See also: Ideal generated by polynomials, Monomial orderings
The objective is to perform a sort of multivariate division of polynomials that has the form[1]
$$f = q_1f_1 + \ldots + q_sf_s + r,$$
where we have multiple quotients—$q_1,\ldots,q_s$—and multiple divisors—$f_1,\ldots, f_s$—and a residual, $r$.
Example 1
We start with a benign case. We will divide $f(x, y) = xy^2+1$ by $f_1(x, y) = xy+1$ and $f_2(x, y) = y+1$. The division looks like this:
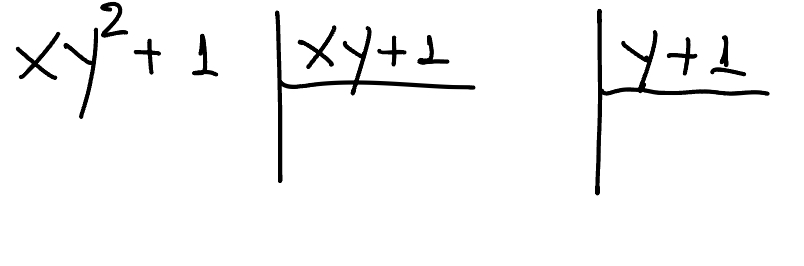
Figure 1. Polynomial to be divided by two other polynomials.
That is, we have two divisors and we'll have two quotients (but one residual).
We use the lex ordering $x > y$. Before we proceed, note
| Term | Multiindex | Degree |
|---|---|---|
| $xy^2$ | $(1, 2)$ | $3$ |
| $xy$ | $(1, 1)$ | $2$ |
| $y$ | $(0, 1)$ | $1$ |
| $1$ | $(0, 0)$ | 0 |
Using the lex ordering we have $xy^2 > xy > y > 1$.
We start the division like we'd do in the univariate case: we identify the leading terms (this is conditioned by the choice of ordering) and divide:
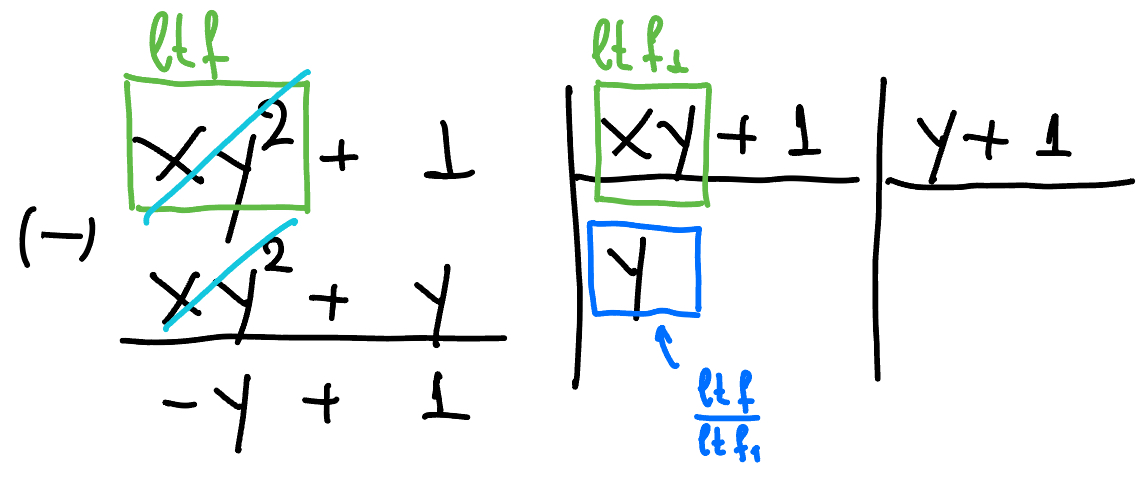
Figure 2. Step 1.
We cannot continue to divide by $xy+1$ because $xy$ does not divide $-y$. We continue with $f_2=y+1$:
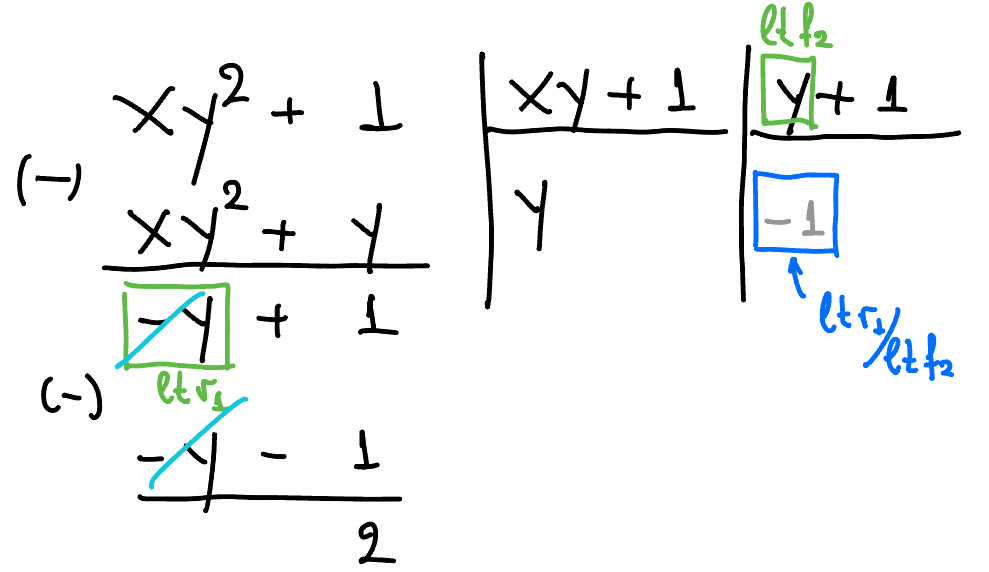
Figure 3. Step 2.
We conclude that
$$xy^2+1 = y(xy+1) + y(y+1) + 2.$$
This was... misleadingly easy!
Example 2
This is a problematic case. We want to divide $f=x^2y+xy^2+y^2$ by $f_1=xy-1$ and $f_2=y^2-1$ in the lexicographic order. We proceed as above, but at some point we get stuck...
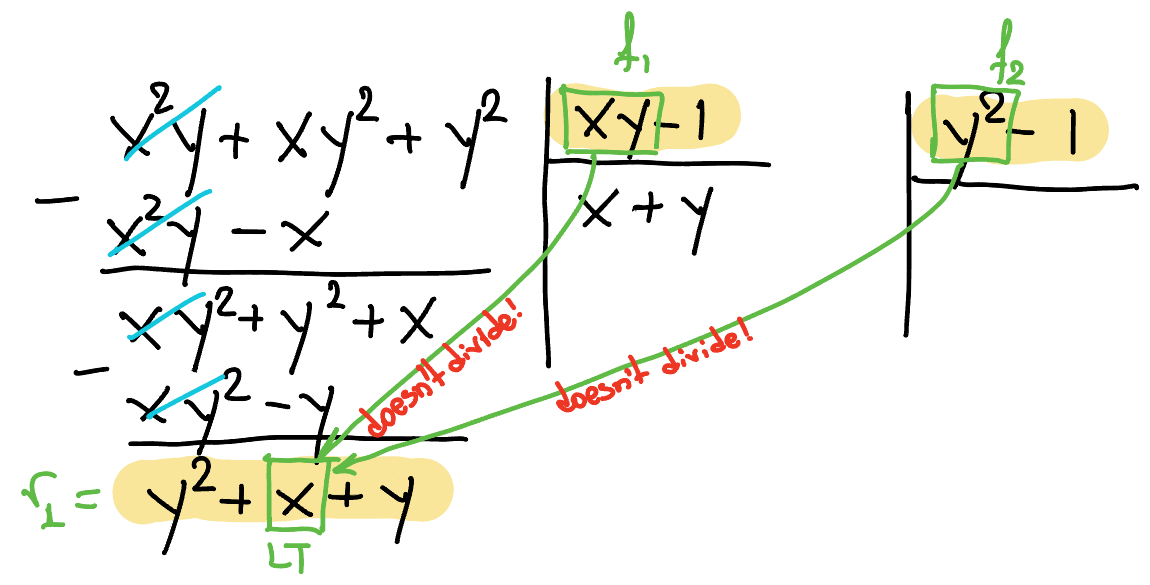
Figure 4. Polynomial division: the issue is that the leading term of $y^2-1$ does not divide the leading term of the remainder (which is $x$).
The problem is that neither $xy$ nor $y^2$ divides the leading term of the current residual, $y^2+x+y$. However, $y^2$ divides a non-leading term: $y^2$. This is unexpected — it would never happen in the univariate case!
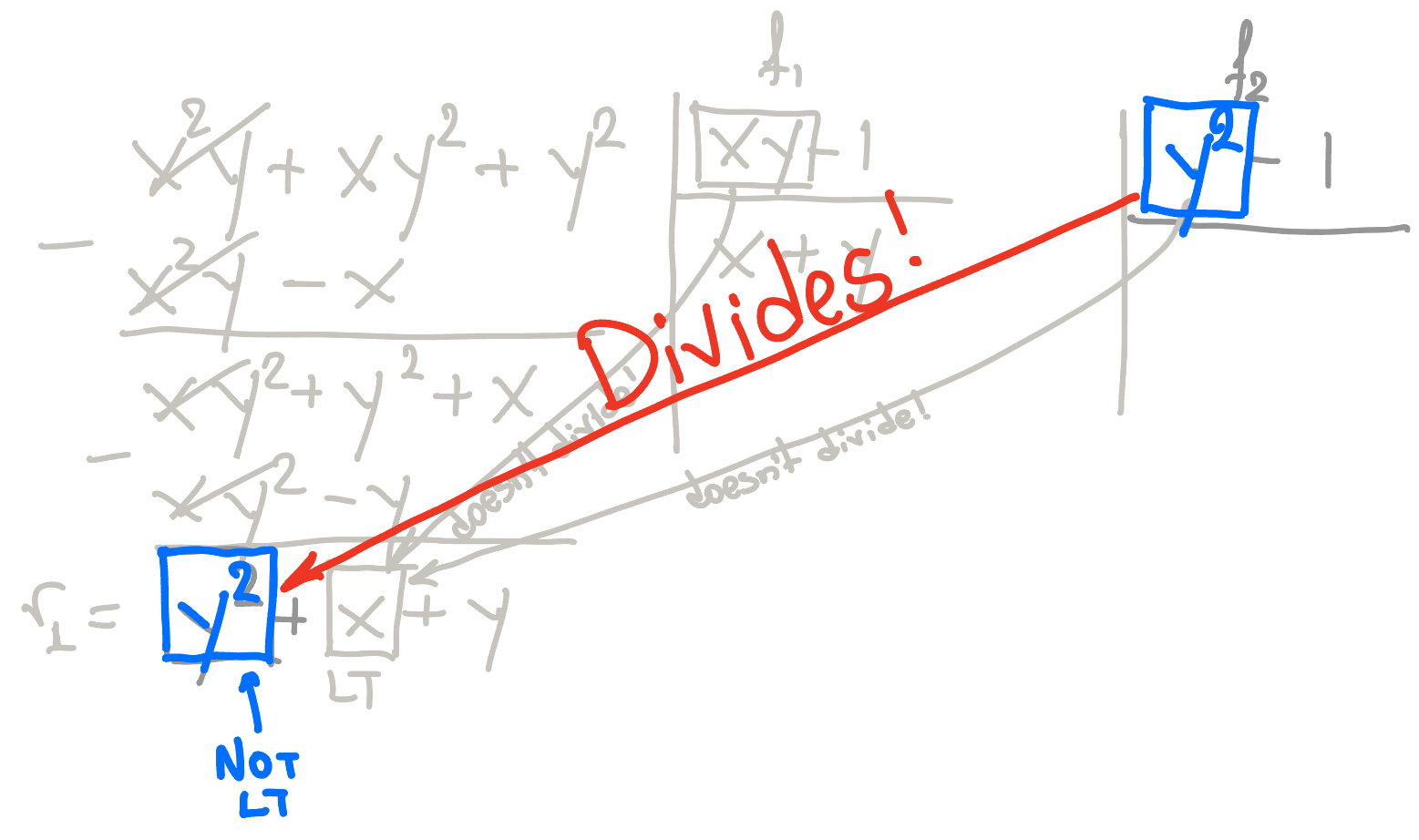
Figure 5. Polynomial division: the divisor divides a non-leading term.
So the "workaround" is to move the leading term ($x$) of $r_1$ to the side and check whether $y^2$ (of $f_2$) divides the residual (having removed the leading term, $x$):
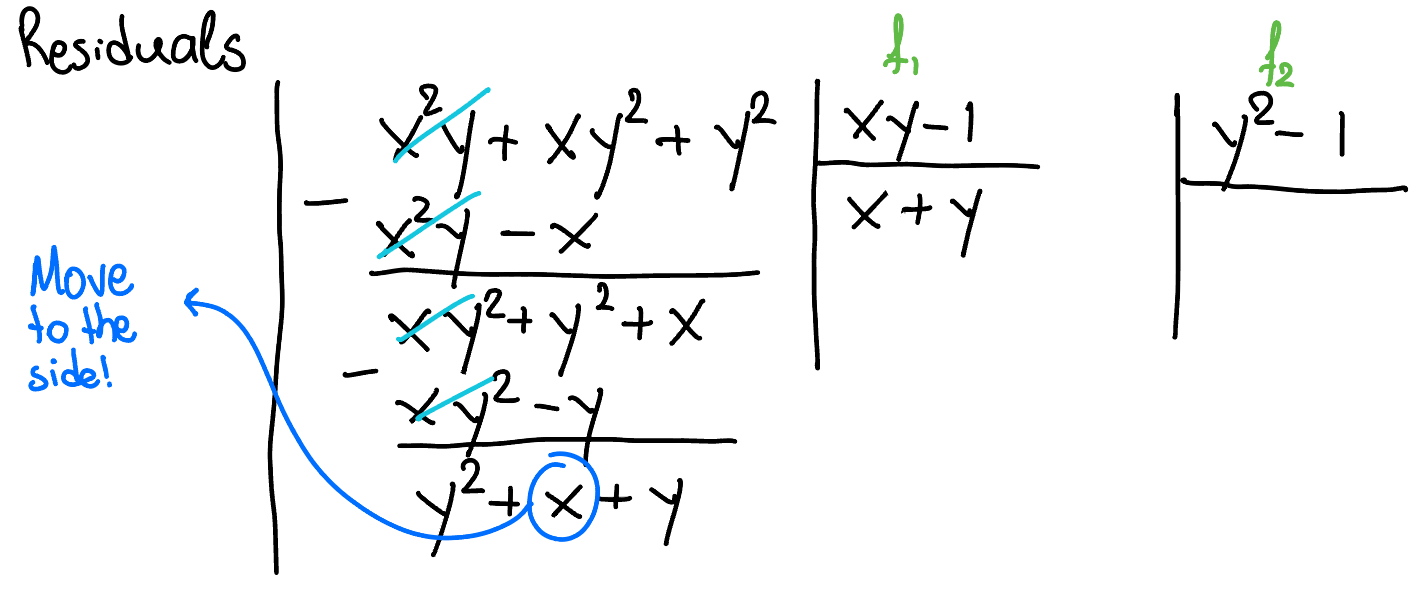
Figure 6. Polynomial division - workaround: setting aside the term of the residual that cannot be divided.
Once we move $x$ to the side we can divide by $y^2-1$:
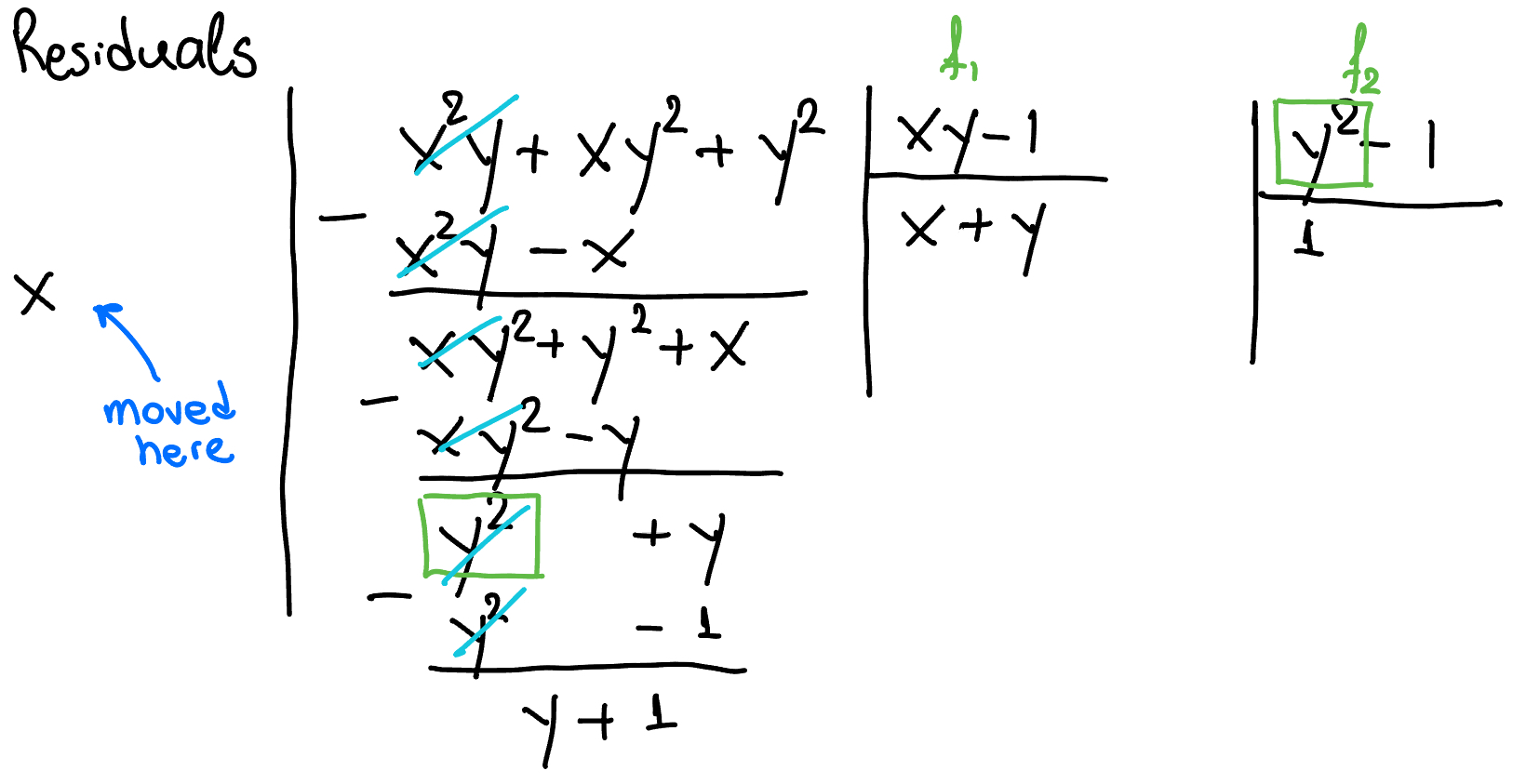
Figure 7. Polynomial division: we can now divide.
Now we should really stop. We have
$$x^2y+xy^2+y^2 = (xy-1)\cdot (x+y) + (y^2-1)\cdot 1 + (x+y+1).$$
A multivariate division algorithm
Cox et al.[1] give this division algorithm:
% Input: f1, ..., fs, f
% Output: q1, .., qs, r
q1 = 0; ...; qs = 0; r = 0
while p ≠ 0 do
i = 1
division_occurred = false
while i ≤ s and division_occurred == false do
if lt(fi) divides lt(p)
qi = qi + lt(p) / lt(fi)
p = p - ( lt(p) / lt(fi) ) * fi
division_occurred = true
else
i = i + 1
if division_occurred == false
r = r + lt(p)
p = p - lt(p)
return q1, ..., qs, r
Conclusion
Let ${}>{}$ be a monomial ordering on $\N^n$ (i.e., on $k[x_1,\ldots, x_n]$), let $f\in k[x_1,\ldots, x_n]$, which we want to divide by $f_1, \ldots, f_s$. The order of $f_1, \ldots, f_s$ is important. Then,
$$f = a_1f_1 + \ldots + a_s f_s + r,$$
where $a_i\in k[x_1,\ldots, x_n]$ for $i=1,\ldots, s$, and
- either $r=0$, or
- $r$ is a polynomial whose monomials are not divisible by any of $\operatorname{lt}(f_1), \ldots, \operatorname{lt}(f_s)$
The polynomial $r$ is called the remainder of the division.
Furthermore, for $a_if_i\neq 0$,
$$\operatorname{multideg}f \geq \operatorname{multideg}(a_if_i),$$
and
$$\operatorname{multideg}f \geq \operatorname{multideg}r.$$
Ideal membership?
If the remainder of a division is zero, we'll have
$$f=a_1f_1+a_2f_2,$$
i.e., $f\in \langle f_1, f_2\rangle$. The problem is that if $r\neq 0$ this doesn't imply that $f\notin \langle f_1, f_2\rangle$. Here's an example:
Suppose we want to divide $f=xy^2-x$ by $f_1=xy+1$ and $f_2=y^2+1$ (in this order and using the lexicographic order). We have
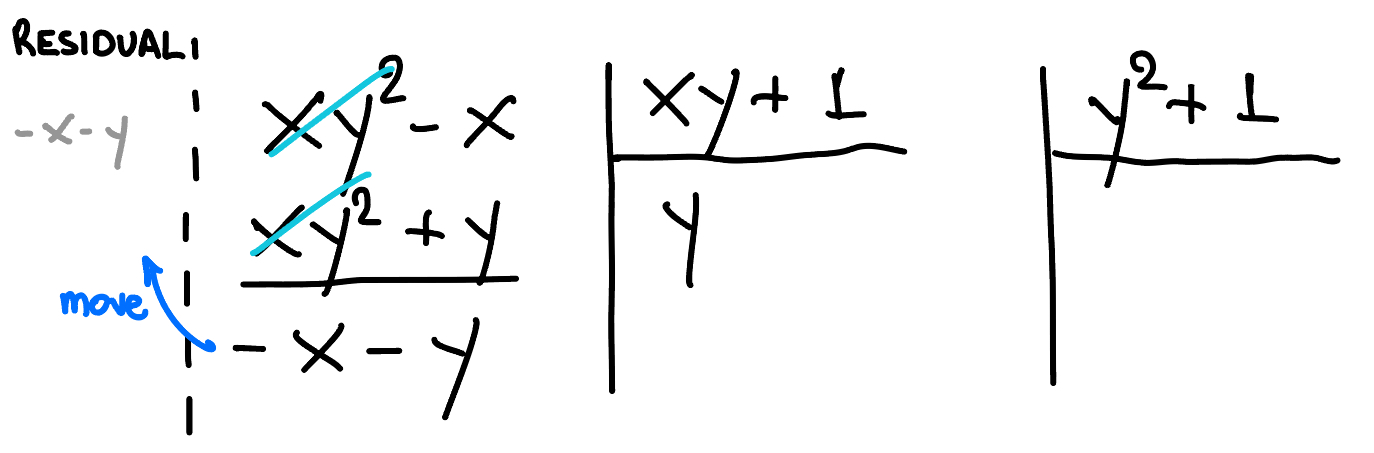
Figure 8. Polynomial division by $f_1$ and $f_2$.
which means that
$$xy^2-x = y(xy+1) + 0(y^2+1) + (-x-y),$$
so we have a nonzero residual. But if we divide by $(f_2, f_1)$ we get a different result.
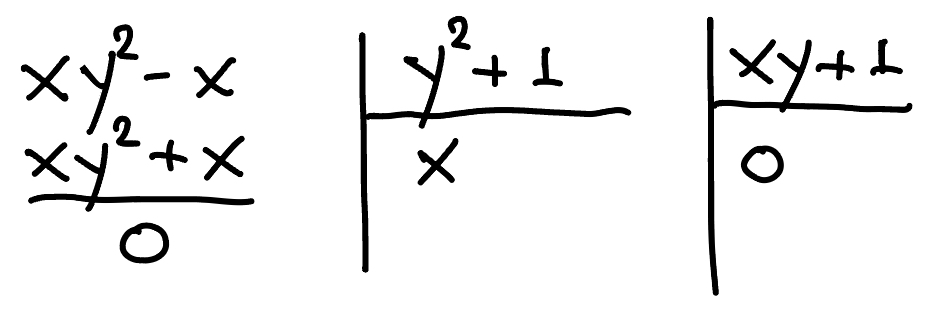
Figure 9. Polynomial division by $f_2$ and $f_1$: different result.
Now the residual is zero. This means that
$$xy^2-x \in \langle y^2+1, xy+1\rangle,$$
but we couldn't have concluded this when we divided by $(f_1, f_2)$.
Exercises
Exercise 1: division. Compute the remainder on division of the given polynomial $f$ by the ordered set $F$ (by hand). Use the `grlex` order, then the `lex` order in each case:
$$f =x^7y^2 +x^3y^2 −y+1, F=(xy^2 −x,x−y^3).$$
Solution. Firstly, let us use the lexicographic order. We write the above polynomials with their terms in descending order.
$$f = x^7y^2 +x^3y^2 −y+1, f_1 = xy^2 −x, f_2 = x - y^3.$$
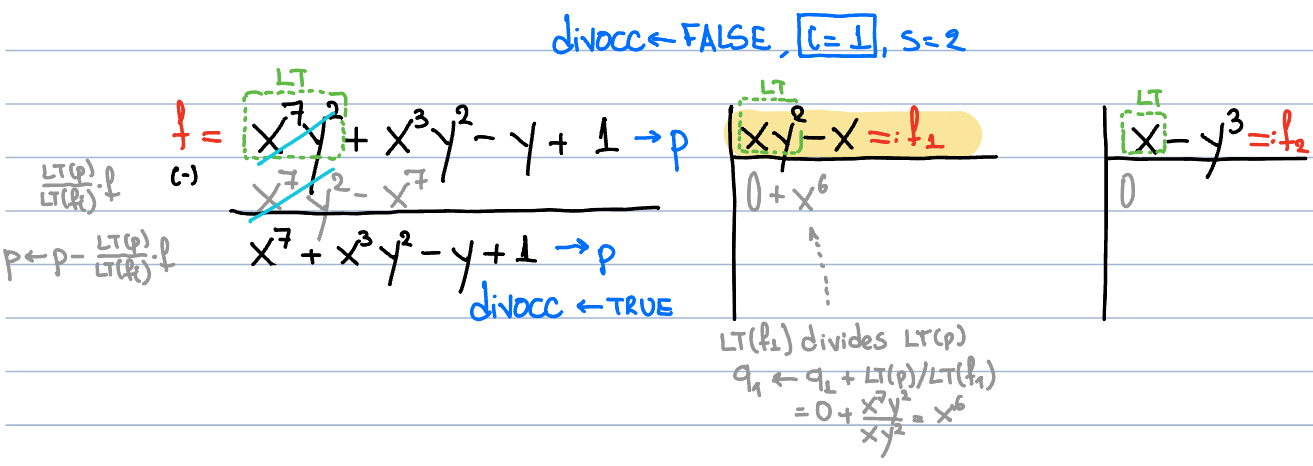
Figure 10. Polynomial division of $f$ by $F$.
Then,
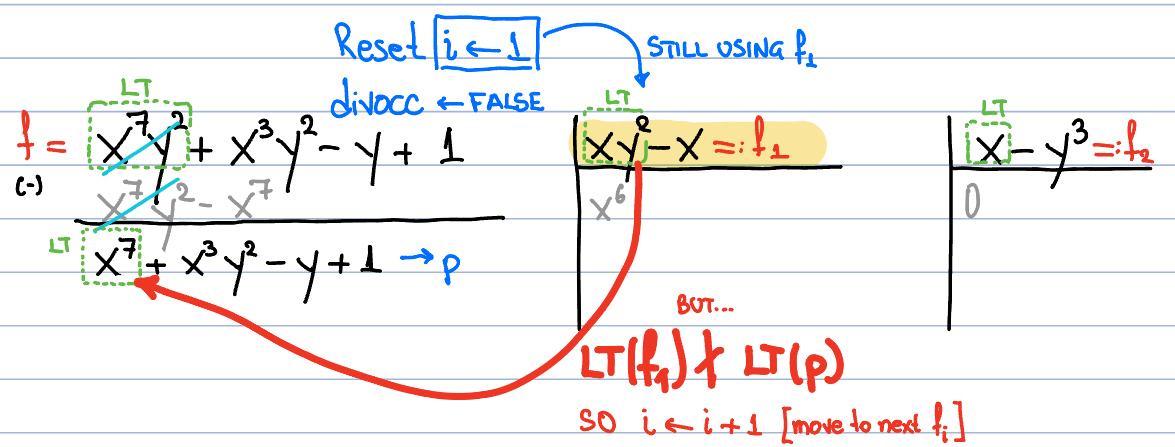
Figure 11. Polynomial division of $f$ by $F$: division is not possible.
since division is not possible we proceed to the the next polynomial, that is, $f_2$,
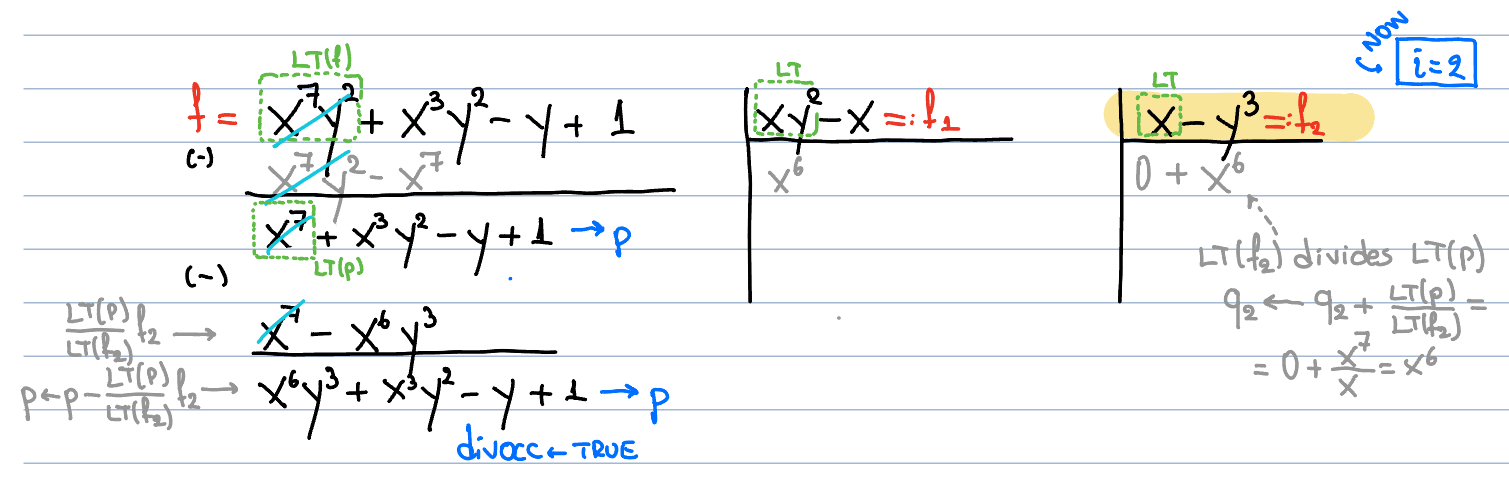
Figure 12. Polynomial division of $f$ by $F$: division is not possible.
The division is successful, so we reset $i$ and we set $i=1$. We don't keep dividing by $f_2$, we continue with the default divisor; here $f_2$ was an alternative divisor (our plan B)...

Figure 13. Polynomial division of $f$ by $F$: division is not possible.
Continuing like this we find that
$$f=q_1f_1 + q_2f_2 + r,$$
where
$$\begin{aligned} q_1 {}={}& x^6 + x^5y + x^4y^2 + x^4 + x^3y + x^2y^2 + 2x^2 + 2xy + 2y^2 + 2, \\ q_2 {}={}& x^6 + x^5y + x^4 + x^3y + 2x^2 + 2xy + 2, \\ r {}={}& 2y^3 -y + 1. \end{aligned}$$
If we perform the division in the order $(f_2, f_1)$ we find
$$f = a_2f_2 + a_1f_1 + \rho,$$
where
$$\begin{aligned} a_2 {}={}& x^6y^2 + x^5y^5 + x^4y^8 + x^3y^{11} + x^2y^{14} + x^2y^2 + xy^{17} + xy^5 + y^{20} + y^8, \\ a_1 {}={}& 0, \\ \rho {}={}& y^{23} + y^{11} -y + 1. \end{aligned}$$
This is a super weird result because both the quotients and the residual seem to be of higher order than $f$, but this is not the case in the lexicographic order. Note that we have large powers of $y$ there—not of $x$. Let's see how the results look like in the graded lexicographic order. If we divide by $(f_1, f_2)$ we get
$$f = b_1f_1 + b_2f_2 + s,$$
where $b_1=x^6+x^2$, $b_2=0$, and $s=x^7 + x^3 -y + 1$.
If we divide by $(f_2, f_1)$ we get the result
$$f=w_2f_2 + w_1f_1 + v,$$
where $w_2=0$, $w_1=x^2+x^2$, and $v=x^7 + x^3 -y + 1$—essentially the same result; there is a symmetry here (not sure whether this holds always for this monomial order, but I doubt it). $\bullet$
Exercise 2: division. Divide $f=xy^2z^2 + xy - yz$ by $f_1=x- y^2$, $f_2=y - z^3$, $f_3=z^2 - 1$. Try different monomial orderings and different orders of the divisors.
In general
$$f=q_1f_1 + q_2f_2 + q_3f_3 + r,$$
Division by $(f_1, f_2, f_3)$ with lex:
$$\begin{aligned} q_1 {}={}& y^2z^2 + y,\\ q_2 {}={}& y^3z^2 + y^2z^5 + y^2 + yz^8 + yz^3 + z^{11} + z^6 - z,\\ q_3 {}={}& z^{12} + z^{10} + z^8 + z^7 + z^6 + z^5 + z^4 + z^3 + z,\\ r {}={}& z. \end{aligned}$$
Again here we see some large powers like 10, 11, and 12.
Division by $(f_3, f_1, f_2)$ with lex:
$$\begin{aligned} q_1 {}={}& y^2 + y,\\ q_2 {}={}& y^3 + y^2z + y^2 + yz + y + 1,\\ q_3 {}={}& xy^2 + y^3z + y^2z^2 + y^2z + y^2 + yz^2 + yz + y + z,\\ r {}={}& z. \end{aligned}$$
Division by $(f_2, f_3, f_1)$ with lex:
$$\begin{aligned} q_1 {}={}& z + 1,\\ q_2 {}={}& xyz^2 + xz^5 + x + yz + y + z^4 + z^3 - z,\\ q_3 {}={}& xz^6 + xz^4 + xz^2 + xz + x + z^5 + z^4 + z^3 + z,\\ r {}={}& z. \end{aligned}$$
Once again, lex gives some large powers.
Division by $(f_1, f_2, f_3)$ with grlex:
$$\begin{aligned} q_1 {}={}& -xz^2,\\ q_2 {}={}& 0,\\ q_3 {}={}& x^2,\\ r {}={}& x^2 + xy - yz. \end{aligned}$$
Division by $(f_3, f_1, f_2)$ with grlex:
$$\begin{aligned} q_1 {}={}& -x,\\ q_2 {}={}& 0,\\ q_3 {}={}& xy^2,\\ r {}={}& x^2 + xy - yz. \end{aligned}$$
Division by $(f_2, f_3, f_1)$ with grlex:
$$\begin{aligned} q_1 {}={}& z + 1,\\ q_2 {}={}& xyz^2 + xz^5 + x + yz + y + z^4 + z^3 - z,\\ q_3 {}={}& xz^6 + xz^4 + xz^2 + xz + x + z^5 + z^4 + z^3 + z ,\\ r {}={}& z. \end{aligned}$$
References
- David A. Cox, John Little, Donal O’Shea, Ideals, Varieties and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, Springer, 2015
- K. Batselier, P. Dreesen, B. De Moor, The geometry of multivariate polynomial division and elimination, SIAM J. Matrix Anal. Appl. 34(1):102-25, 2013, link