The main aim of Hilbert's basis theorem is to address the "ideal description problem" which is
Ideal description problem. Does every ideal $I \subseteq k[x_1, \ldots, x_n]$ have a finite basis? Can we write $I = \langle f_1, \ldots, f_s\rangle$ for some polynomials $f_1, \ldots, f_s\in k[x_1, \ldots, x_n]$?
Hilbert's basis theorem gives an affirmative answer. It also generalises Dickson's lemma which states that every monomial ideal is finitely generated.
Overview
This note is based on[1].
Theorem 0: Hilbert's basis theorem (for ordinary people). Hilbert's basis theorem states that a polynomial ideal over a field has a finite generating set.
More generally (not just about polynomial rings), the rings that have this property are the Noetherian rings. A more general statement of Hilbert's basis theorem is
Theorem 1: Hilbert's basis theorem. If $R$ is a Noetherian ring, then $R[x]$ is also Noetherian.
Leading terms
Given a polynomial ideal $I$, different from $\{0\}$, and a monomial ordering $<$, we define
$$\operatorname{lt}(I) = \{cx^\alpha : \exists f\in I \setminus\{0\}: \operatorname{lt}(f) = cx^\alpha\}.$$
In simple words, this is the set of leading terms of the elements of $I$ (with respect to $<$).
The leading terms of $I$ play an important role in division.
If $I$ is generated by $\{f_1, \ldots, f_s\}$, i.e.,
$$I = \langle f_1, \ldots, f_s\rangle,$$
it is not true that
$$\langle \operatorname{lt}(I)\rangle = \langle \operatorname{lt}(f_1), \ldots, \operatorname{lt}(f_s)\rangle.$$
However, $\operatorname{lt}(f_i) \in \operatorname{lt}(I)$, so $\langle \operatorname{lt}(f_1), \ldots, \operatorname{lt}(f_s)\rangle \subseteq \langle \operatorname{lt}(I)\rangle$.
Before we proceed we need to recall two important things:
- $\langle \operatorname{lt}(f_1), \ldots, \operatorname{lt}(f_s)\rangle$ is a monomial ideal
- to tell whether a monomial $x^\beta$ is a member of a monomial ideal it suffices to check whether it is divisible by a monomial in that ideal
Example 1. To see that $\langle \operatorname{lt}(f_1), \ldots, \operatorname{lt}(f_s)\rangle \subsetneq \langle \operatorname{lt}(I)\rangle$ let's consider the polynomials $f_1, f_2 \in k[x, y]$ with $f_1 = x^3 - 2xy$ and $f_2 = x^2y - 2y^2 + x$. Define $I=\langle f_1, f_2\rangle$. Then, take the monomial $h = x^2$ and using grlex divide $h$ by $(f_1, f_2)$. We see that
$$x^2 = xf_1 + yf_2,$$
so $h\in \langle f_1, f_2\rangle = I$. However, $h$ is not divisible by $\operatorname{lt}(f_1) = x^3$ and it is not divisible by $\operatorname{lt}(f_2) = x^2y$ meaning that $h \notin \langle \operatorname{lt}(f_1), \operatorname{lt}(f_2)\rangle.$ $\bullet$
Theorem 2. For every ideal $I\subseteq k[x_1, \ldots, x_n]$, $\langle \operatorname{lt}(I)\rangle$ is a monomial ideal.
Proof. Easy.
Theorem 3. For every ideal $I\subseteq k[x_1, \ldots, x_n]$, there are polynomials $g_1, \ldots, g_t$ such that
$$\langle \operatorname{lt}(I)\rangle = \langle \operatorname{lt}(g_1), \ldots, \operatorname{lt}(g_t)\rangle.$$
Proof. From Theorem 2, $\langle \operatorname{lt}(I)\rangle$ is a monomial ideal, so from Dickson's lemma it is finitely generated, i.e., $\langle \operatorname{lt}(I)\rangle = \langle \operatorname{lt}(g_1), \ldots, \operatorname{lt}(g_t)\rangle$ for some $g_1, \ldots, g_t \in k[x_1, \ldots, x_n]$. $\Box$
Proof Hilbert’s basis theorem
We will prove Theorem 0. Here's an overview of the proof:
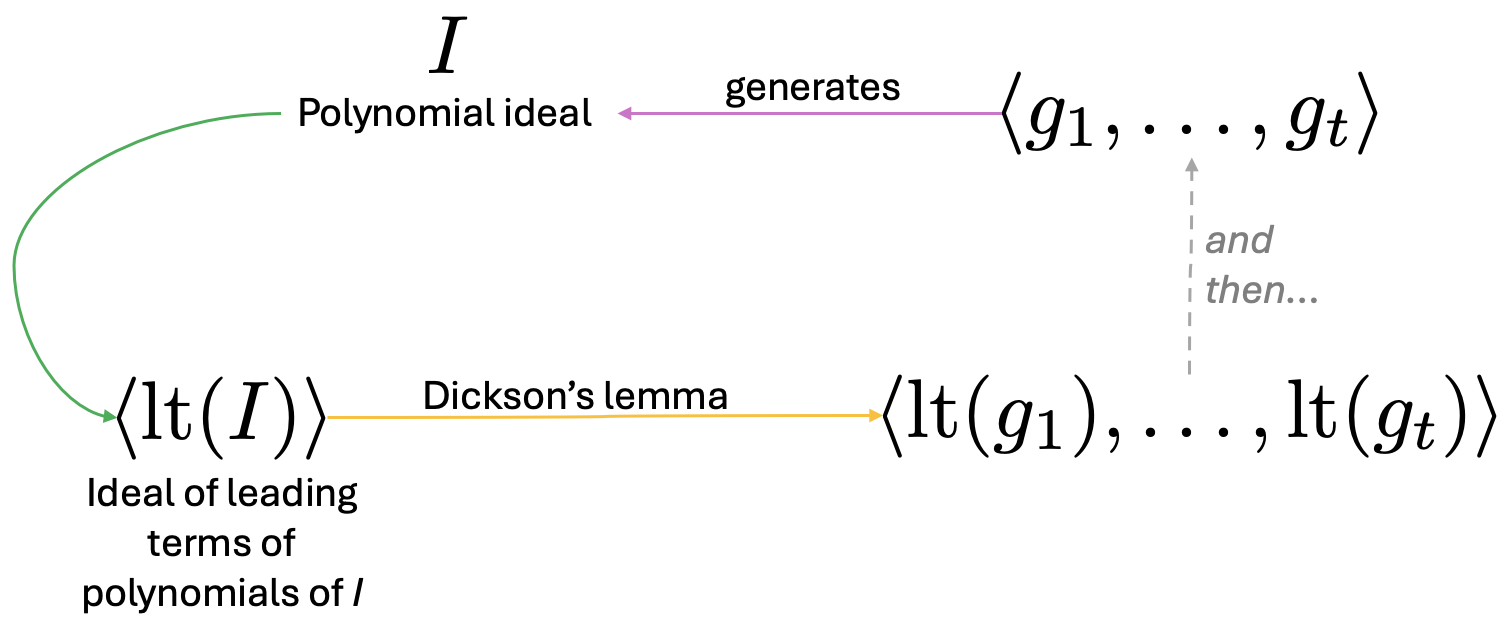
Figure 1. Overview of proof of Hilbert's basis theorem: from $I$ we construct $\langle \operatorname{lt}(I)\rangle$, which, by Theorem 3 has a finite basis (from Dickson's lemma).
The claim is that
$$I=\langle g_1, \ldots, g_t\rangle.$$
Since $g_1, \ldots, g_t \in I$, we can establish that $\langle g_1, \ldots, g_t\rangle \subseteq I$. For the converse, take $f\in I$ and divide it by $(g_1, \ldots, g_t)$:
$$f = q_1g_1 + \ldots +q_tg_t + r.$$
We claim that $r=0$. Note that
$$r = f - q_1g_1 - \ldots - q_tg_t,$$
so $r\in I$. If $r\neq 0$, then $\operatorname{lt}(r) \in \operatorname{lt}(I) = \langle \operatorname{lt}(g_1), \ldots, \operatorname{lt}(g_t)\rangle,$ so $\operatorname{lt}(r)$ is divisible by at least one of $\operatorname{lt}(g_i)$, which contradicts the properties of the residual. $\Box$
Gröbner bases
In the proof of Hilbert's basis theorem we came up with a basis $\{g_1, \ldots, g_t\}$ such that $\langle \operatorname{lt}(I)\rangle = \langle \operatorname{lt}(g_1), \ldots, \operatorname{lt}(g_t)\rangle$. Such a basis (for $I$) is called a Gröbner basis. As we saw in the proof above, every ideal $I$ has a Gröbner basis and a Gröbner basis is a basis (it generates the ideal).
References
- David A. Cox, John Little, Donal O’Shea, Ideals, Varieties and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, Springer, 2015; see Section 2.4 (monomial ideals and Dickson’s lemma)
- Nice lecture notes, 6.S897 Algebra and Computation, Ideal Membership Problem and Gröbner Basis, Instructor: Madhu Sudan , Scribe: Chennah Heroor, 2015, accessed on 19 July 2024.