See first: Monomial orderings
Why monomial ideals?
A few reasons:
- It is easier to work with monomial ideals(1) rather than with general ideals; it is also more natural to work with monomials(3)
- What is true for monomial ideals is often true for general ideals(2); this is due to Hilbert’s basis theorem
- We can study general ideals in terms of monomial ideals
Intro: divisibility of monomials
A monomial $x^\beta$ is divisible by $x^\alpha$—where $x=(x_1, \ldots, x_n)$ is a multivariate indeterminate and $\alpha, \beta\in\N^n$ are multiindices—if there is a monomial $x^\gamma$, $\gamma\in\N^n$, such that
$$x^\beta = x^\alpha x^\gamma,$$
meaning $\beta = \alpha + \gamma$, i.e., $\beta-\alpha = \gamma$, which imposes the requirement that
$$\beta - \alpha \in \N^n.$$
Equivalently, $x^\alpha {}\mid{} x^\beta$ iff $\beta \in \alpha + \N^n$. This can be illustrated geometrically in $\N^2$ as shown in Figure 1 (4).
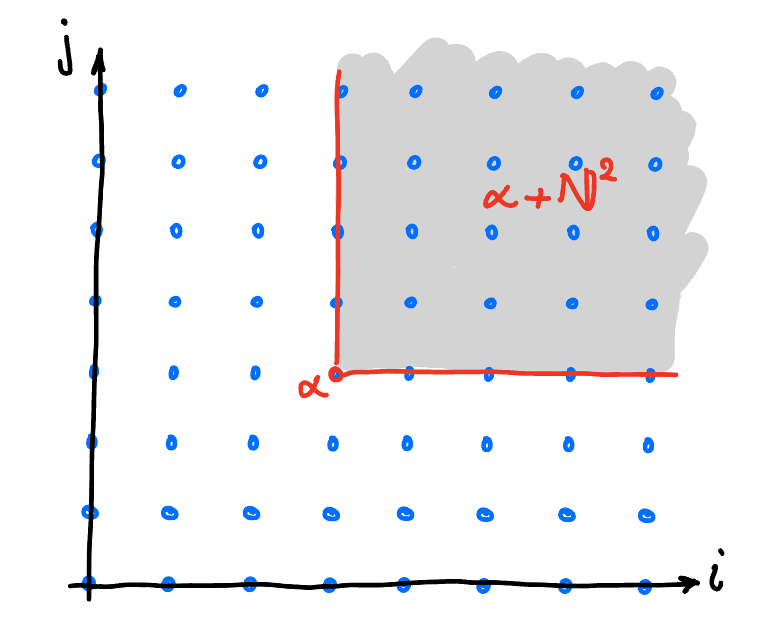
Figure 1. A multiindex $\alpha\in\N^2$; $\alpha$ divides all the multiindices in the shaded area.
In a way, we can say that the multiindices in the shaded area in Figure 1 are "above" $\alpha$.
The set of multiindices that are divisible by either $\alpha$ or $\alpha'$ is the set $(\alpha + \N^2) \cup (\alpha' + \N^2)$, which is illustrated below. The term $x^\beta$, with $\beta \in (\alpha + \N^2) \cup (\alpha' + \N^2)$, is divisible by $x^\alpha$ *or* $x^{\alpha'}$. This is illustrated in Figure 2.
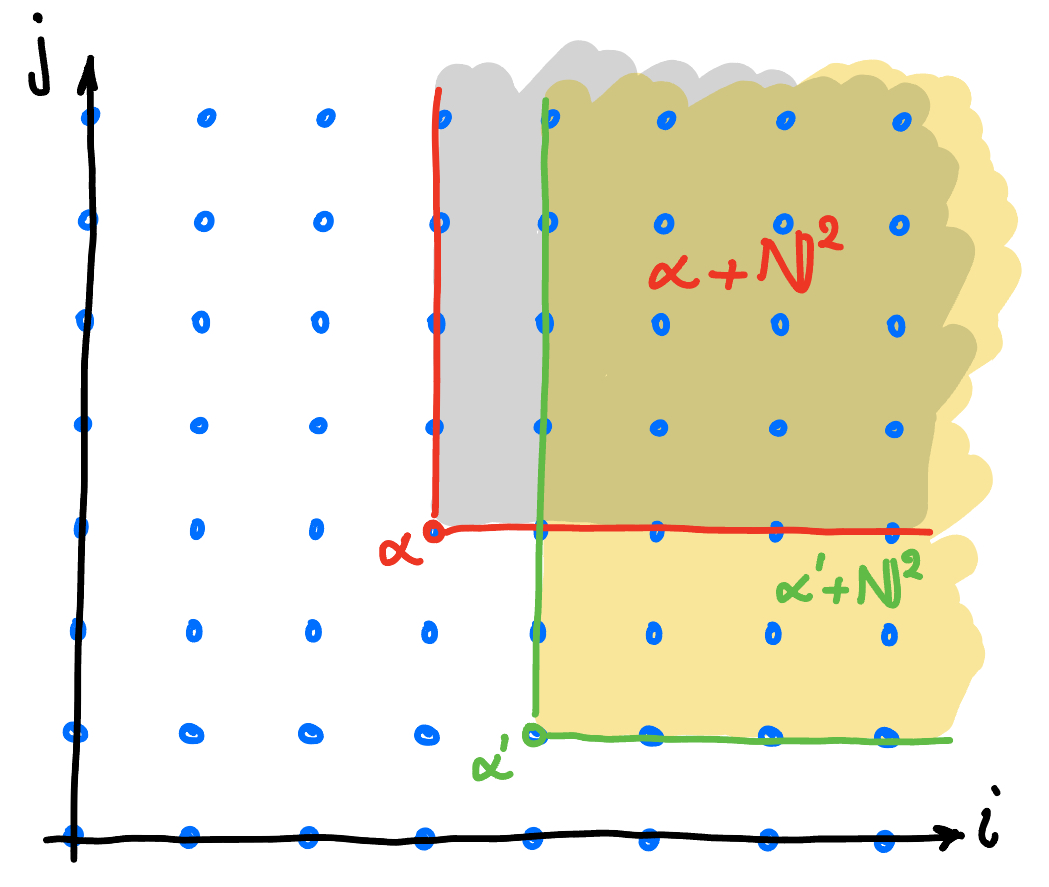
Figure 2. Set of multiindices divisible by either $x^\alpha$ or $x^{\alpha'}$.
In Figure 3 we see a situation where $\alpha$ is divisible by $\alpha'$.
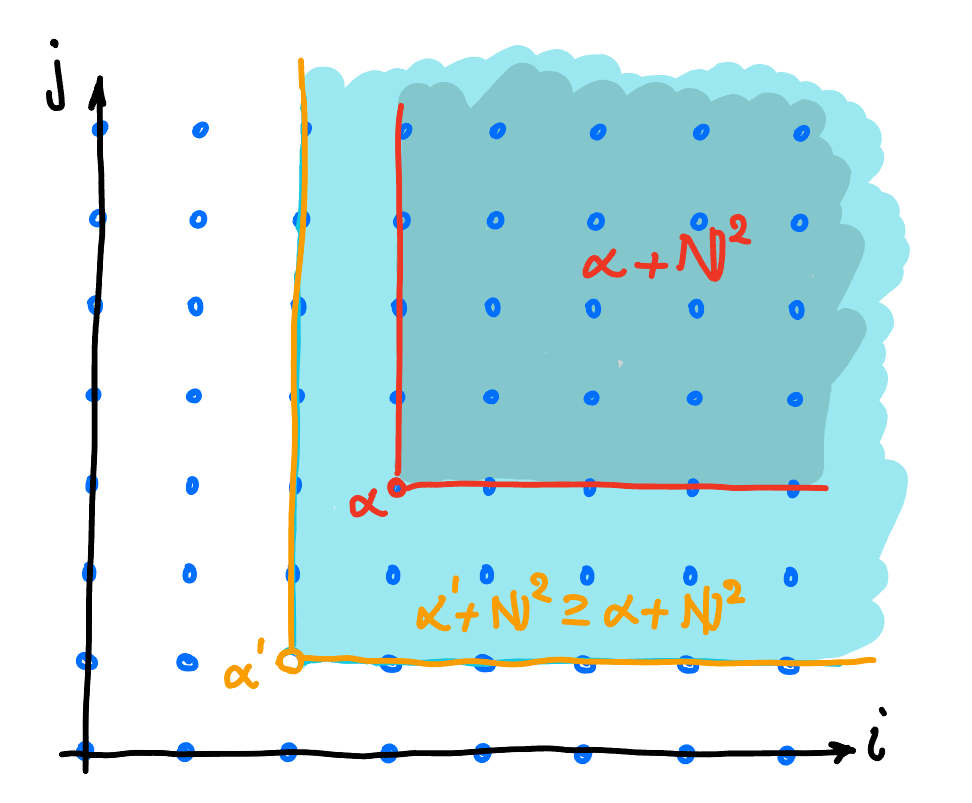
Figure 3. Here $\alpha + \N^2 \subset \alpha' + \N^2$.
Divisibility of monomials and monomial ideals
In general, a monomial ideal is defined as follows
Definition 1: Monomial ideal. A monomial ideal is a set of the form
$$I = \left\{\sum_{i=1}^{s}h_{i} x^{\alpha_i}; h_\alpha \in k[x_1,\ldots, x_n], \alpha_i \in A\right\},$$
where $A\subseteq \N^n$ (can be infinite). In other words, $I$ consists of polynomials, which are finite sums of the form $\sum_{i=1}^{s}h_{\alpha_i} x^{\alpha_i}$ for some multiindices $\alpha_i\in A$.
We can write
$$I = \langle x^\alpha; \alpha \in A\rangle,$$
with some abuse of notation as an ideal generated by polynomials has been defined to be a finite combination of the generators, whereas here $A$ is possibly infinite. The above notation for $I$ is meant as a shorthand for Definition 1.
Let us first prove the following
Proposition 1. Let $I = \langle x^\alpha; \alpha \in A\rangle$ be a monomial ideal. Then, $x^\beta\in I$ iff $x^\beta$ is divisible by $x^\alpha$ for some $\alpha\in A.$
Proof. Firstly, the easy part: suppose $x^\beta$ is divisible by $x^\alpha$ for some $\alpha\in A,$ i.e., there is $\gamma\in\N^n$ such that $x^\alpha x^\gamma = x^\beta$, and trivially $x^\gamma\in I$.
For the converse, suppose $x^\beta\in I$. This means that there are $h_1, \ldots, h_s\in k[x_1, \ldots, x_n]$ such that
$$\underbrace{h_1x^{\alpha_1} + \ldots + h_s x^{\alpha_s}}_{\text{polynomial}} = \underbrace{{}\;\;{}x^\beta{}\;\;{}}_{\text{monomial}}.\tag{$*$}$$
The trick here is the on the lhs we have a polynomial (what seems to be a general polynomial), but on the right we have a monomial, so $h_1x^{\alpha_1} + \ldots + h_s x^{\alpha_s}$ is a monomial!
Suppose
$$h_i = \sum_{j=1}^{M}\kappa_{j}^{i}x^{\lambda_{j}^{i}},$$
for all $i=1,\ldots, s$, where $\kappa^i_j \in k$ and $\lambda_{j}^{i}\in\N^n$. Then, from ($*$) we have
$$\sum_{i=1}^{s}\sum_{j=1}^{M}\kappa_{j}^{i}x^{\lambda_{j}^{i}+\alpha_i} = x^\beta,$$
and because the thing on the lhs is a monomial, there is an $i^*$ such that
$$\beta = \alpha_{i^*} + \text{something},$$
so that $x^{\alpha_{i^*}} {}\mid{} x^\beta$. $\Box$
The following proposition provides conditions for a polynomial to be in a monomial ideal
Proposition 2: Membership of polynomial in monomial ideal. Let $I$ be a monomial ideal (see Definition 1) and $f\in k[x_1,\ldots, x_n]$. Tfae:
- $f\in I$
- Every term of $f$ is in $I$
- $f$ is a $k$-linear combination of monomials from $I$
This implies that a monomial ideal is characterised by its monomials. Note that a monomial ideal does not contain only monomials, but it is identified by its monomials. Convenient!
Proof. The only interesting part is to show that (1) $\implies$ (2). Since $f\in I$ it can be written as $f=\sum_{i=1}^{s}h_ix^{\alpha_i}$ (for some $s$) for $h_i\in k[x_1, \ldots, x_n]$, so $h_i$ can be written as $h_i = \sum_{j=1}^{\kappa_i}c_j^i x^{\beta_j^i},$ where the $\beta_j^i$ are multiindices. Therefore, $f$ can be written as
$$f = \sum_{i=1}^{s}\sum_{j=1}^{\kappa_i}c_j^ix^{\alpha_i + \beta_j^i},$$
and since $\alpha_i + \beta_j^i \geq \alpha_i$, $x^{\alpha_i} {}\mid{} x^{\alpha_i + \beta_j^i}$, so, from Proposition 1, the terms $x^{\alpha_i + \beta_j^i}$ are in $I$. This completes the proof. $\Box$
Demo. To demonstrate Proposition 2, have a look a Figure 4 below
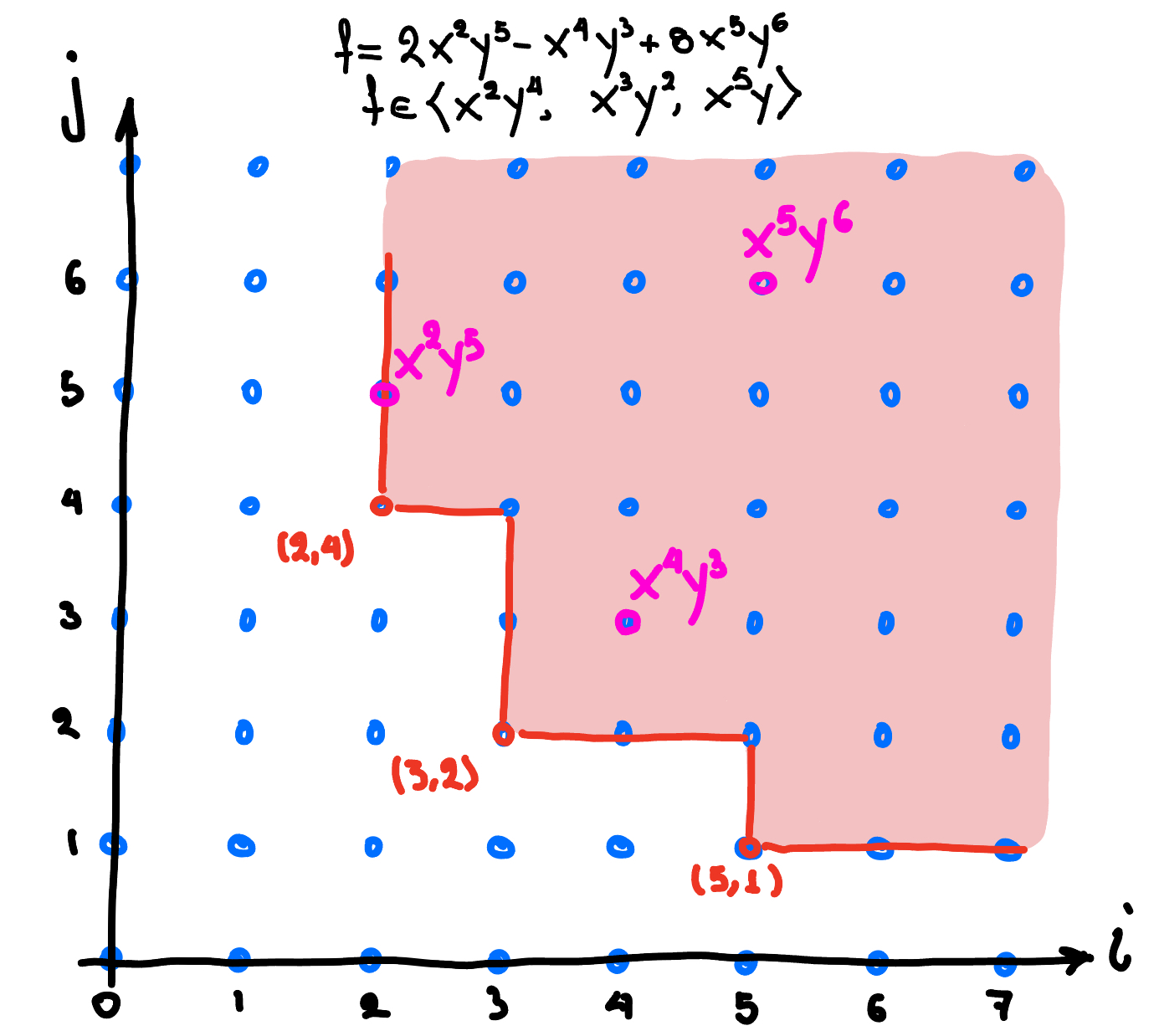
Figure 4. The shaded are corresponds to the monomial ideal generated by $x^2y^4, x^3y^2, x^5y$. We see that $f = 8x^5y^6 - x^4y^3 + 2x^2y^5$ is in this ideal.
By division of $f$ by the generators of the ideal we have
$$f = (8x^3y^2 + 2y)\cdot \textcolor{red}{x^2y^4} + (-xy) {}\cdot{} \textcolor{red}{x^3y^2}.$$
Important corollary. Two monomial ideals are the same if they contain the same monomials.
Don't forget that a monomial ideals contains both monomials and general polynomials. This corollary allows us to compare ideals based on their monomials only!
Monomial ideal membership: We now have an easy way to tell whether a polynomial is in a monomial ideal, $I=\langle m_1, m_2, \ldots, m_s\rangle$. It suffices to check whether each of the terms of the polynomial is divisible by *one* of the generators of the ideal.
Note: Geometry of monomial ideal. We now know what the geometry of a monomial ideal is. A monomial ideal—to the extent that is characterised uniquely by the monomials it contains—it identified by a subset of $\N^n$.
Dickson's lemma
The following is a remarkable result about monomial ideals. It says that they're never too large!
Dickson's lemma states that monomial ideals are finitely generated. We can see connections with Noetherian rings and it is a special case of Hilbert's basis theorem.
Dickson's lemma. Monomial ideals are finitely generated.
The proof is important because it is constructive and reveals how to construct a finite basis for a monomial ideal.
Proof. The proof is by induction. Let's start with $n=1$ (univariate polynomials). Then, $I$ is generated by monomials $x^\alpha$, with $\alpha\in \N$. Let $\beta$ by the smallest of these integers (which exists); then $\beta\leq \alpha$, so $x^\beta \mid x^\alpha$, therefore, $I=\langle x^\beta\rangle$.
In Cox et al.(4) they perform a general inductive step, but for the sake of clarity and simplicity let's look at $\N^2$. Suppose that $I\subseteq k[x, y]$ is a monomial ideal and we want to find (finitely many) generators (monomials) for $I$.
We construct an ideal $J\subseteq k[x]$ such that $x^\alpha \in J$ iff there is $m\in\N$ such that $x^\alpha y^m \in I$. This is like a projection of $I$ onto $k[x]$.
We know that $J$ is finitely generated: $J=\langle x^\beta\rangle$ for some $\beta \in \N$ (see beginning of proof). Then, $x^\beta y^m \in I$ for some $m\in \N$.
For $l=0,\ldots,m-1$ consider ideals $J_l\subseteq k[x]$ such generated by $x^\gamma$ such that $x^\gamma y^l \in I$. This means that $J_l$ is a slice of $I$ where $y$ is at a power $l$. $J_l$ has a finite basis, so $J_l = \langle x^{\gamma_l}\rangle$.
Claim: $I$ is generated by $I' = \{x^{\gamma_0}, x^{\gamma_1}y, x^{\gamma_2}y^2, \ldots, x^{\gamma_{m-1}}y^{m-1}, x^\beta y^m\}.$
Indeed, if $g$ is a monomial in $I$, it is divisible by all elements of $I'$. From Proposition 1 and the above corollary, we can show that $I=I'$. $\Box$
Endnotes
- Wikipedia, Monomial ideals, accessed on 6 July 2024
- Cornell, lecture notes on monomial ideals and Dickson’s lemma, accessed on 6 July 2024
- J. Herzog and T. Hibi, Monomial ideals (book), Springer, 2011; difficult to read
- David A. Cox, John Little, Donal O’Shea, Ideals, Varieties and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, Springer, 2015; see Section 2.4 (monomial ideals and Dickson’s lemma)