Our familiar trace operator is a linear map with the property $\mathrm{tr}(AB)=\mathrm{tr}(BA)$ for all square matrices $A$ and $B$, or, what is the same $\mathrm{tr}(xy^\intercal)=y^\intercal x$ for all vectors $x$ and $y$. In fact, if $f$ is a linear map with this property, then it is the trace up to scaling.
To generalise this, we start by observing that $y^\intercal x$ can be thought of as (the linear map) $y$ acting on $x$ to return a scalar, that is $y^\intercal$ can be thought of as an element of the dual space $(\R^n)^*$. Secondly, the trace could be seen as an operator $\mathrm{tr}(y^\intercal, x)$ (an operator $\mathrm{tr}:(\R^n)^*\times\R^n \R\to\R$), which is linear in $x$ and in $y^\intercal$ (i.e., bilinear); from the universal property of tensor products, we can look at the trace as a linear map $\mathrm{tr}:(\R^n)^*\otimes \R^n\to\R$.
We may now define the trace in the context of tensor products.
Definitions
Given a vector space $V$ over a field $k$ we define the trace operator to be the linear map
$$\mathrm{tr}: V^* \otimes V\to k,$$
where for $a\in V^*$ and $u\in V$,
$$\mathrm{tr}(a\otimes u) = a(u).$$
Having defined this for pure tensors, for general tensors we have
$$\mathrm{tr}\left(\sum_i c_i(a_i \otimes u_i)\right) = \sum_i c_i a_i(u_i).$$
Alternatively, leveraging the universal property of tensor products, we can define the bilinear map $\mathrm{tr}': V^*\times V \to k$ with
$$\mathrm{tr}'(\phi, x) = \phi(x).$$
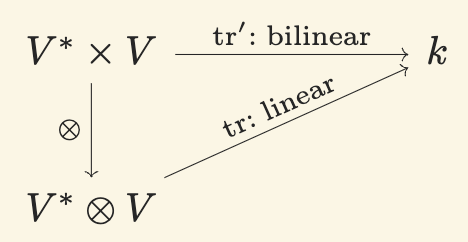
Figure 1. Universal property for the trace map.
Interpretation in the finite-dimensional case
We know that in the finite-dimensional case, where $\dim V = n$, $V^*\otimes V \cong {\rm Hom}(V, V)$ with isomorphism a function which, for pure tensors, is defined as
$$\Phi(a\otimes v)(\xi) = a(\xi)v.$$
Since this $\Phi: V^*\otimes V \to {\rm Hom}(V, V)$ is linear, when applied to general tensors it gives
$$\Phi\left(\sum_i \lambda_i (a_i\otimes v_i)\right)(\xi) = \sum_i \lambda_i a_i(\xi)v_i.$$
To define the inverse, suppose that a basis for $V$ is $B_V = \{e_1, \ldots, e_n\}$. The corresponding dual basis is $B_{V^*} = \{e_1^*, \ldots, e_n^*\}$. The inverse is
$$\Phi^{-1}(\phi) = \sum_{i}e_i^* \otimes \phi(e_i).$$
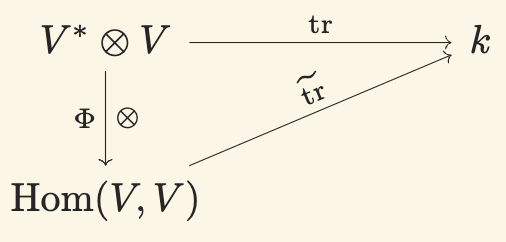
Figure 2. The trace of a tensor can be seen as the trace of an endomorphism.
The linear map $\widetilde{\mathrm{tr}}:{\rm Hom}(V, V) \to k$ is defined as
$$\widetilde{\mathrm{tr}} = \mathrm{tr} \circ \Phi^{-1}.$$
Finite-dimensional vector spaces
If $V$ is a finite vector space with basis $B_V = \{e_1, \ldots, e_n\}$, then the dual basis, of $V^*$, is $B_{V^*} = \{e_1^*, \ldots, e_n^*\}$. The tensor space has basis vectors $B_{V^*\otimes V} = \{e_i^* \otimes e_j\}_{i,j=1}^{n}$ and $\dim (V^*\otimes V) = n^2$. The trace has been defined as a linear map $\mathrm{tr}: V^* \otimes V\to k$, with $\mathrm{tr}(a\otimes u) = a(u)$, so it suffices to see how it works on the basis of the tensor space. It is
$$\mathrm{tr}(e_i^*\otimes e_j) = e_i^*(e_j) = \delta_{i,j},$$
where $\delta_{i,j}$ is the Kronecker delta.
The matrix case
Theorem 1. For $A\in\R^{n\times n}$ (that is, $A:\R^n\to\R^n$),
$$\widetilde{\mathrm{tr}} A = \sum_{i=1}^{n} A_{ii}.$$
Proof. Here $A\in\R^{n\times n}$ is treated as a linear map $A:\R^n\to \R^n$. We have
$$\Phi^{-1}(A) = \sum_{i=1}^{n} e_i^* \otimes Ae_i,$$
and
$$\mathrm{tr}(\Phi^{-1}(A)) = \mathrm{tr}\left(\sum_{i=1}^{n} e_i^* \otimes Ae_i\right) = \sum_{i=1}^{n} e_i^*(Ae_i) = \sum_{i=1}^{n} A_{ii}.$$
This completes the proof. $\Box$
Trace of dual map
Theorem 2. Assume again that $V$ is finite dimensional. Let $T\in{\rm Hom}(V, V)$ and let $T'$ be the dual map. Then,
$$\mathrm{tr}(T) = \mathrm{tr}(T').$$
Before we proceed with the proof, note that
$${\rm Hom}(V, V) \cong V^* \otimes V \cong V^* \otimes (V^*)^* \cong (V^*)^* \otimes V^* \cong {\rm Hom}(V^*, V^*).$$
Proof. Suppose that a basis of $V$ is $\{e_1,\ldots, e_n\}$ and let the dual basis be $\{e_1^*, \ldots, e_n^*\}$. The canonical embedding of the basis of $V$ onto $V^{**}$ is $e_i^{**}$. We have
$$\begin{aligned}\mathrm{tr} T {}={}& \mathrm{tr} \left( \sum_i e_i^* \otimes Te_i\right) \\ {}={}& \sum_i \mathrm{tr}(e_i^* \otimes Te_i) \\ {}={}& \sum_i e_i^* (Te_i) \\ {}={}& \sum_i T'(e_i^*)(e_i) \\ {}={}& \sum_i e_i^{**}(T'(e_i^*)) \\ {}={}& \sum_i \mathrm{tr} (e_i^{**} \otimes T'(e_i^*)) \\ {}={}& \mathrm{tr} T', \end{aligned}$$
which completes the proof. $\Box$
Trace on a tensor product space
Here we will look at the trace on $V\otimes V^*$.
If $V^{**} \cong V$ (e.g., finite-dimensional case), then $V\otimes V^{*} \cong (V^*)^* \otimes V^*$ so, for $x\in V^{**}$ and $a\in V^*$ we can define
$$\mathrm{tr}(x\otimes a) = x(a) = a(x) = \mathrm{tr}(a\otimes x),$$
where here we have identified $x\in V^{**}$ with $x\in V$ via the isomorphism $V^{**} \cong V$.
Trace of tensor product and composition
From Kim Exercise 3.1.R on tensors and assuming $f, g\in {\rm End}(V)$ can be written as $f = a\otimes x$ and $g = b\otimes y$[^1] we have the diagram
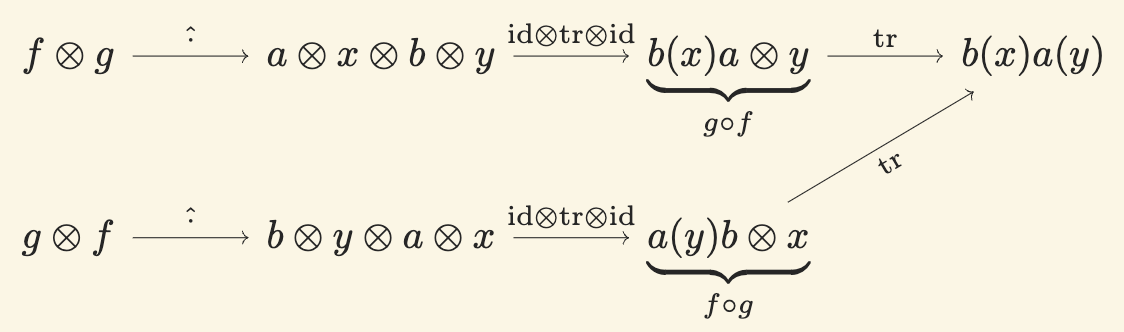
Figure 3. Trace and tensor products.
This means
$$\mathrm{tr}((\mathrm{id} \otimes \mathrm{tr} \otimes \mathrm{id})(f\otimes g)) {}={} \mathrm{tr}((\mathrm{id} \otimes \mathrm{tr} \otimes \mathrm{id})(g\otimes f))$$
Equivalently
$$\mathrm{tr}(g\circ f) {}={} \mathrm{tr}(f\circ g).$$
More generally
$$\mathrm{tr}(g\circ f \circ h) {}={} \mathrm{tr}(h\circ f \circ g) {}={} \mathrm{tr}(g \circ h\circ f).$$
At the same time, if we treat $f\in {\rm End}(V)$ as an element of $V^* \otimes V$ we can talk about its trace. If $f = a\otimes x$ and $g=b\otimes y$, then
$$\mathrm{tr}(f\otimes g) = b(x) a(y) = \mathrm{tr}(g\otimes f).$$