About
In this post we will state and prove the Hahn-Banach theorem and the three separating theorems. All results will be stated for general topological vector spaces (normed spaces are a special case). All vector spaces in this post are taken over the field of real numbers.
Read also:
- Support functions of convex sets
Preliminaries
We assume that the reader is familiar with the concept of a topological vector space (TVS).
Let \(X\) be a TVS. Recall that a set \(A \subseteq X\) is said to be balanced if \([-1, 1]A \subseteq A\). Of course \(0\in A\). Note that balanced sets are symmetric (\(-A = A\)).
A set \(A\) is said to be absorbing if for every \(x\in X\) there is a \(c_0 > 0\) such that \(x \in cA\) for all \(c\in{\rm I\!R}\) with \(|c| \geq c_0\). In simple words, a set is absorbing if it can be inflated to include any point \(x\in X\) and once it absorbes \(x\) as we keep inflating it, it will keep containing \(x\).
We will recall a fact from the theory of TVS that we will be using a lot in what follows. If \(X\) is a TVS, the origin has a topological base of balanced and absorbing sets.
Positive sublinear functionals
Definition 1 (Positive sublinear functional). Let \(X\) be a vector space. A \(p:X\to{\rm I\!R}\) is called a positive sublinear functional (PSLF) if the following conditions are satisfied
- \(p\) is nonnegative valued on \(X\)
- \(p\) is positively homogeneous on \(X\), that is, \(p(\lambda x) = \lambda p(x)\) for all \(\lambda\geq 0\) and \(x\in X\)
- \(p\) is sublinear, that is, \(p(x+y) \leq p(x) + p(y)\)
Note that PSLFs are not necessarily symmetrix (\(p(-x)\) is not equal to \(p(x)\)) and it is not necessary that \(x=0\) whenever \(p(x) = 0\).
Note that if \(p\) is an PSLF and \(\lambda < 0\), then \(p(x) \leq -p(-\lambda x).\)
Proposition 2 (Continuity of PSLFs). Let \(X\) be a topological vector space (TVS) and \(p:X\to{\rm I\!R}\) is an PSLF. Then, the following are equivalent
- \(p\) is continuous
- \(p\) is continuous at \(0\)
- \(p\) is bounded in a neighbourhood of \(0\)
Proposition 3 (PSLFs have convex sublevel sets). Let \(X\) be a TVS and \(p:X\to{\rm I\!R}\) is an PSLF. Then, its sublevel sets, \(\{x: p(x) \leq a\}\), are convex.
Proof. Straightforward. \(\blacksquare\)
Next, we will show that any linear functional that is bounded above by a continuous PSLF, is continuous.
Proposition 4 (Continuity of linear functionals). Let \(X\) be a TVS, \(p:X\to{\rm I\!R}\) is an PSLF, \(A: X\to{\rm I\!R}\) is linear, and
$$A(x) \leq p(x),$$
for all \(x\in X\). If \(p\) is continuous, then \(A\) is continuous.
Zorn’s lemma
In this section we'll state Zorn's lemma, which is a very useful tool in functional analysis (and not only) with numerous applications. Zorn's lemma can be proven using the axiom of choice (in fact, it is equivalent to the axiom of choice).
We will state Zorn's lemma here without a proof. We will later use it to prove the Hahn-Banach theorem. Firstly, we need to state some definitions.
Definition 5 (Partial order). Let \(A\) be a nonempty set. A relation, \(\leq\), is a partial order on \(A\) if it satisfies the following properties
- (Reflexivity) \(a \leq a\) for all \(a\in A\)
- (Antisymmetry) \(a \leq b\) and \(b \leq a\) implies \(a = b\) for all \(a, b\in A\)
- (Transitivity) \(a \leq b\) and \(b \leq c\) implies that \(a \leq c\) for all \(a, b, c \in A\)
Note that for a given set \(A\) and a partial order \(\leq\) on \(A\) it is not necessary that either \(a\leq b\) or \(b\leq a\). For example, that the partial order \(\preceq\) on the set of symmetric matrices where \(A \preceq B\) means that \(B-A\) is positive semidefinite. There can be matrices \(A\) and \(B\) such that neither \(A \preceq B\) nor \(B \preceq A\).
Definition 6 (Chain). Let \(A\) be a nonempty set equipped with a partial order \(\leq\). A set \(B\ subseteq A\) is said to be a chain if for every \(a,b\in B\), either \(a\leq b\) or \(b\leq a\).
As an example, take \(A={\rm I\! R}^n\) and for \(x,y \in {\rm I\! R}^n\) let \(x\leq y\) if and only if \(x_i \leq y_i\) for all \(i\). Take \(x_0 \in {\rm I\! R}^n\), \(x_0 \neq 0\). The set \(B={\rm I\! R} x_0 = \{\lambda x_0; \lambda \in {\rm I\! R}^n\}\) is a chain.
Definition 7 (Maximal element). Let \(A\) be a nonempty set equipped with a partial order \(\leq\). An element \(M \in A\) is said to be a maximal element of \(A\) if for all \(x\in A\),
$$m \leq x \Rightarrow x = m.$$
As an example, take again \(A={\rm I\! R}^n\) and for \(x,y \in {\rm I\! R}^n\) let \(x\leq y\) if and only if \(x_i \leq y_i\) for all \(i\). Take \(B\) to be the unit-ball of the Euclidean norm. Then any \(m \in {\rm I\! R}^n\) with \(\|m\|=1\) is a maximal element of \(B\). Note also that \(A\) does not have any maximal elements.
Definition 8 (Upper boun of a chain). Let \(A\) be a nonempty set equipped with a partial order \(\leq\) and let \(B\subseteq A\) be a chain. An element \(m \in A\) is said to be an upper bound of the chain if \(x \leq m\) for every \(x\in B\).
As a simple example, take \(A={\rm I\! R}\) with the standard order, \(\leq\), and the chain \(B = (0, 1)\). Then \(m=2\) is an upper bound; \(m=1\) is another upper bound of \(B\).
We will now state Zorn's lemma (without a proof).
Lemma 9 (Zorn's lemma). Let \(A\) be a nonempty set equipped with a partial order \(\leq\) and every chain has an upper bound. Then, \(A\) has a maximal element.
The Hahn-Banach Theorem
The Hahn-Banach theorem is without doubt one of the most important theorems in functional analysis with numerous applications the most notable of which are the separating theorems. The proof of the Hahn-Banach theorem is of remarkable elegance!
Theorem 10 (Hahn-Banach Theorem). Let \(X\) be a TVS and \(p: X \to {\rm I\!R}\) is an PSLFs. Let \(Y\subseteq X\) be a subspace of \(X\) and a linear functional \(f:Y\to{\rm I\!R}\) is such that
$$f(y) \leq p(y),$$
for all \(y\in Y\). Then, there exists a linear functional \(\hat{f}: X \to {\rm I\!R}\) such that
- \(\hat{f}\) extends \(f\), i.e., \(\hat{f}(y) = f(y)\) for all \(y\in Y\)
- \(\hat{f}(x) \leq p(x)\) for all \(x \in X\)
Note that the linear functional \(\hat{f}\) of the Hahn-Banach theorem is guaranteed to be continuous by virtue of Proposition 4.
Note that we could have stated the Hahn-Banach theorem on a linear space instead of a TVS, but the topology is necessary to be able to talk about the continuity of \(\hat{f}\).
Minkowski functional
We will now introduce the Minkowski functional. The Minkowski functional is an PSLF which is defined using a convex set. Let us give the definition.
Definition 11 (Minkowski functional). Let \(X\) be a TVS and \(K\subseteq X\) is a convex set that contains zero in its interior (\(0 \in \mathrm{int}\; K\)). We define the Minkowski functional as
$$p_K(x) = \inf \left\{ \lambda > 0 : \frac{x}{\lambda} \in K\right\} = \inf \left\{ \lambda > 0 : x \in \lambda K\right\}.$$
Note that the set \(\{ \lambda > 0 : x / \lambda \in K\}\) is nonempty because every neighbourhood of the origin is absorbing, so \( \mathrm{int}\; K\) is an absrobing set, so \(K\) is also absorbing.
We will now show that the Minkowski functional of a \(K\) as in Definition 11 is an PSLF.
Proposition 12 (Minkowski functional is continuous PSLF). Let \(X\) be a TVS and \(K\subseteq X\) is a convex set that contains zero in its interior (\(0 \in \mathrm{int}\; K\)), and let \(p_K\) be the Minkowski functional of \(K\). Then \(p_K\) is a continuous PSLF.
The Minkowski functional of a convex set \(K\) allows us to obtain a complete understanding of the topological properties of \(K\). The following result allows us to use the Minkowski of \(K\) to determine the interior, closure and boundary of \(K\).
We will first introduce the following convenient notation:
$$\begin{aligned}[p_K < 1] {}={}& \{x\in X: p_K(x) < 1\}, \\ [p_K \leq 1] {}={}& \{x\in X: p_K(x) \leq 1\}, \\ [p_K = 1] {}={}& \{x\in X: p_K(x) = 1\}.\end{aligned}$$
Proposition 13 (Topological properties of convex sets). Let \(X\) be a TVS and \(K\) is a convex set with \(0 \in \mathrm{int}\; K\) and let \(p_K\) be the Minkowski functional of \(K\). Then,
- \(\mathrm{int}\; K = [p_K < 1]\)
- \(\mathrm{cl}\; K = [p_K \leq 1]\)
- \(\partial K = [p_K {}={} 1]\)
Proposition 14 (Minkowski functional of convex set). Let \(X\) be a TVS and \(K\) is a convex set with \(0 \in \mathrm{int}\; K\). Then,
$$p_{\mathrm{int}\; K} = p_{K} = p_{\mathrm{cl}\; K}.$$
Using Propositions 13 and 14 we can prove the following surprising topological result for convex sets.
Corollary 15 (Topological property of convex sets). Let \(X\) be a TVS and \(K\) is a convex set with \(0 \in \mathrm{int}\; K\). Then,
$$\mathrm{cl}\; \mathrm{int}\; K {}={} \mathrm{cl}\; K.$$
Convexity is a necessary assumption of Corollary 15. As a counterexample, let \(X\) be a normed space, let \(\mathcal{B}\) be the unit norm ball, \(0 \neq x_0\in X\) and take \(K = \mathcal{B} \cup {\rm I\!R} x_0\), which is not convex. You can verify that \(\mathrm{cl}\; \mathrm{int}\; K {}\subsetneq{} \mathrm{cl}\; K.\)
Convex separating theorems
The Minkowski functional and the Hahn-Banach theorem allow us to prove the famous separating theorems or separating hyperplane theorems or hyperplane separation theorems for convex sets.
We say that a nonzero continuous linear functional \(f: X \to {\rm I\!R}\) separates a set \(K\) and a point \(x_0\) if \(f(x) \leq f(x_0)\) for all \(x\in K\). Equivalently, we can write this as \(\sup f(K) \leq f(x_0)\). We say that \(f\) separates \(K\) and \(x_0\) strictly if the inequality is strict. Similarly, we say that \(f\) separates two sets \(K\) and \(L\) if \(\sup f(K) \leq \inf f(L)\).
We will state three separating theorems that assert the existence of such separating continuous linear functionals. The first separating theorem is about the separation of a convex set from a point. The second separating theorem is about the separation of two convex sets, and the third one is about the strict separation of two convex sets.
Observe that $f$ separates (strictly) two sets $K$ and $L$ (not necessarily convex) if and only if it separates $K-L$ from $\{0\}$. That said, the most fundamental separation theorem is the first separating theorem that allows us to separate a point from a convex set (under certain conditions).
First separating theorem
Let us state the first separating theorem that allows us to separate a point from a convex set using a linear function.
Theorem 16 (First separating theorem). Let \(X\) be a TVS and \(K\) is a convex set with a nonempty interior. Let \(x_0 \notin \mathrm{int}\; K\). Then there is a nonzero continuous linear functional, \(f: X \to {\rm I\!R}\), that separates \(x_0\) from \(K\), that is
$$\sup f(K) {}\leq{} f(x_0).$$
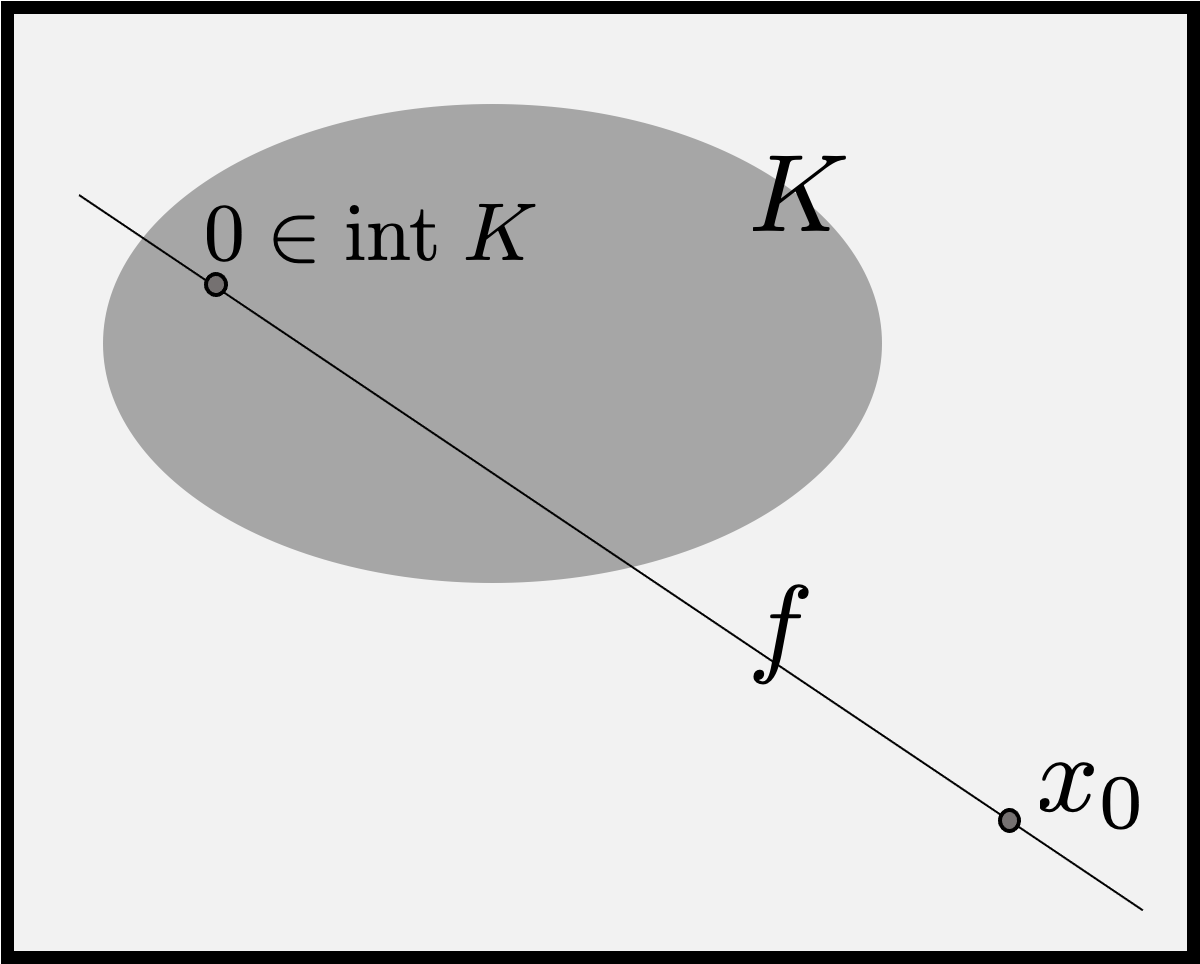
Figure 1. We first define a linear function, \(g\), on \(Y = {\rm I\!R}x_0\) and use the Hahn-Banach theorem to extend it to the entire \(X\).
In the finite-dimensional case, \(X = {\rm I\!R}^n\), linear functions \(f: X \to {\rm I\!R}\) have the form of an inner product, that is, \(f(x) = c^\intercal x\) and the separation of a point \(x_0\in X\) from a convex set \(K\) with a nonempty interior reads
$$\sup_{x\in K} c^\intercal x \leq c^\intercal x_0 \Leftrightarrow \delta^*_K(c) \leq c^\intercal x_0,$$
where \(\delta^*_K\) is the support function of \(K\).
Second separating theorem
The second separating theorem allows us to separate two convex sets.
Theorem 17 (Second separating theorem). Let \(X\) be a TVS and \(K, L\) be two convex sets, \(K\) has a nonempty interior and \(\mathrm{int}\; K \cap L = \emptyset\). Then there is a nonzero continuous linear functional, \(f: X \to {\rm I\!R}\), that separates \(K\) from \(L\), that is
$$\sup f(K) {}\leq{} \inf f(L).$$
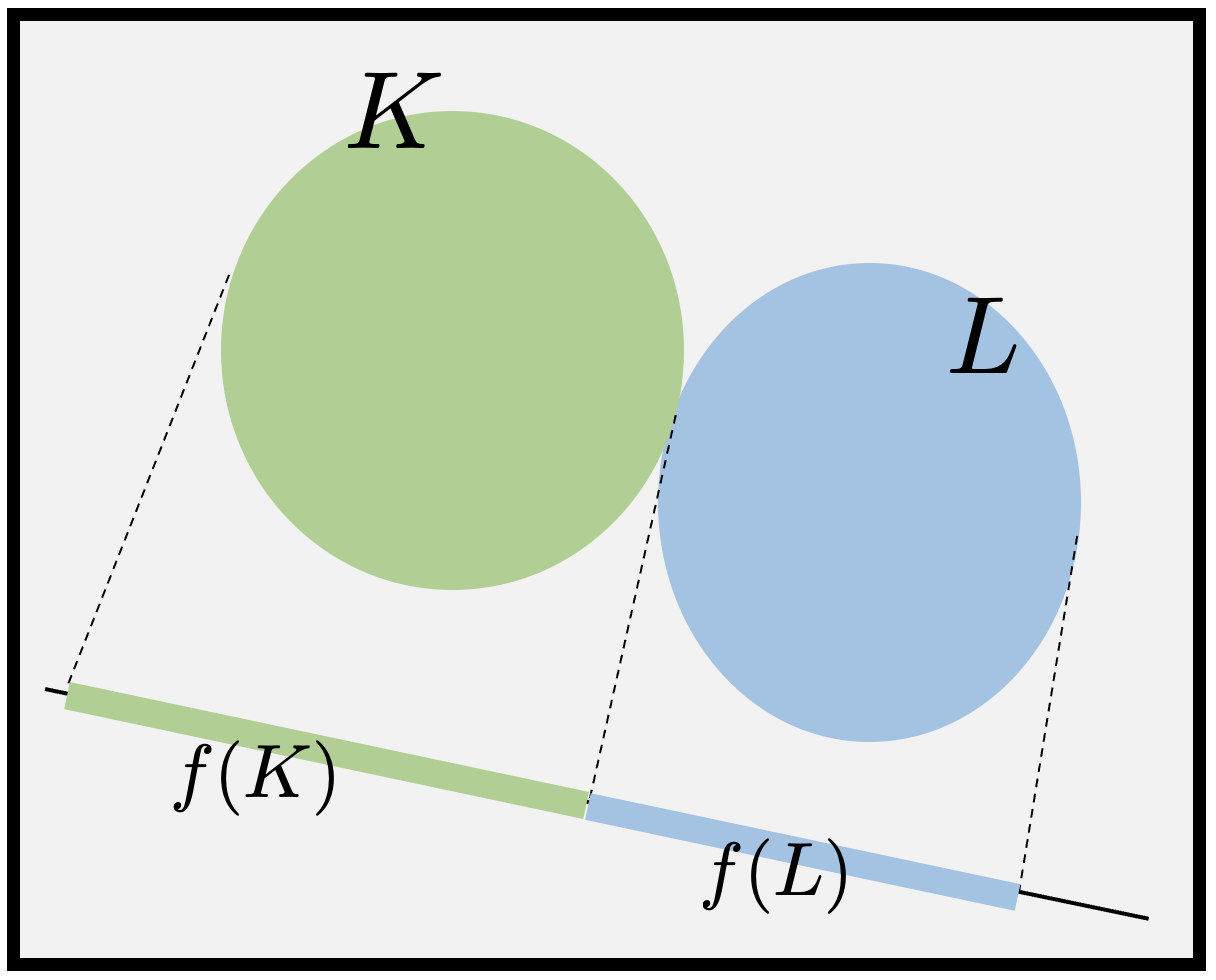
Figure 2. Second separating theorem.
Third separating theorem
For the third separating theorem we will need to assume that \(X\) is a locally convex TVS. A TVS is called locally convex if it has a basis of neighbourhoods of the origin consisting of convex sets.
According to Proposition 4.1.12 in these lecture notes by Maria Infusino (University of Konstanz), every locally convex TVS has a basis of neighbourhoods of the origin consisting of open, absorbing, balanced, convex sets.
Theorem 18 (Third separating theorem). Let \(X\) be a locally convex TVS, \(L\) is a nonempty closed convex set, \(K\) is a nonempty compact convex set and
$$K \cap L = \emptyset.$$
Then, there is a linear continuous functional \(f:X\to{\rm I\!R}\) that separates the two sets strictly.
Next we will show that every closed convex set in a locally convex TVS can be written as an intersection of halfspaces. Recall that a halfspace is a set of the form
$$H = \{x \in X {}:{} f(x) \leq a\} = f^{-1}((-\infty, a]),$$
where \(f: X \to {\rm I\!R}\) is a continuous linear functional.
Proposition 19 (Representation of convex sets). Let \(X\) be a locally convex TVS, and \(K\) is a nonempty closed convex set. Then \(K\) can be written as the intersection of a famiily of halfspaces.
Endnotes
- In Theorem 16 we required that \(K\) has an interior point. Following [3], we can instead impose a weaker assumption, namely, that \(K\) has an internal point. The notions of interior and internal points coincide in fintie-dimensional spaces. More about this in a separate post.
- We can say more about separation in Banach spaces. Of course, things are simpler in \({\rm I\!R}^n\) and finite-dimensional spaces. More posts on this topic will follow.
References
- M. Fabian, P. Habala, P. Hájek, V. Montesinos Santalucía, J. Pelant, and V. Zizler, Functional analysis and infinite-dimensional geometry, Springer, 2001
- N. Bourbaki, Elements of mathematics: topological vector spaces (Chap 1-5), Springer, 2003
- C.D. Aliprantis and K.C. Border, Infinite Dimensional Analysis: A Hitchhiker’s guide, third edition, Springer, 2006