In this post we presented a number of separating theorems on topological vector spaces. Here we will make use of the second separation theorem, which in the case of finite-dimensional spaces is dubbed the hyperplane separation theorem and the assumption of a nonempty interior can be dropped.

We recommend that the reader reads first the following posts

Separation Theorem

Let us start by stating the following result.

Theorem 1 (Hyperplane separation theorem). Let \(K, L\) be two convex sets in ${\rm I\!R}^n$ and \(K \cap L = \emptyset\). Then there is a nonzero vector $c \in {\rm I\!R}^n$ such that

$$\sup_{x\in K} c^\intercal x {}\leq{} \inf_{x\in L} c^\intercal x.\tag{1}$$

Note that the supremum on the left hand side of Equation (1) is the support function of $K$ evaluated at $c$ and the right hand side is

$$\inf_{x\in L} c^\intercal x = - \sup_{x\in L} -c^\intercal x = -\delta_{L}^{*}(-c).$$

The separation condition of Theorem 1 can be equivalently written as: there is $c \in {\rm I\!R}^n$ such that

$$\delta_{K}^{*}(c) \leq -\delta_{L}^{*}(-c).\tag{2}$$

Since $\delta_{L}^{*}(-c) = \delta_{-L}^{*}(c)$, Equation (2) can be written as

$$\delta_{K}^{*}(c) \leq -\delta_{-L}^{*}(c).\tag{3}$$

In the case where both $K$ and $L$ are cones, Equation (3) is equivalent to

$$\delta_{K^\circ}(c) \leq -\delta_{(-L)^{\circ}}(c) \Leftrightarrow c \in K^\circ \cap (-L)^\circ.\tag{4}$$

Polar of finitely generated cone

Let $A\in{\rm I\!R}^{m\times n}$ and its columns be

$$A = \begin{bmatrix}a_1 & \cdots & a_n\end{bmatrix}.$$

We say that the set $C$ is a finitely generated cone, generated by the vectors $a_1, \ldots, a_n$ if it is

$$\begin{aligned}C {}={}& \mathrm{cone}(\{a_1, \ldots, a_p\}) \\ {}={}&\left\{ \sum_{i=1}^{n} y_i a_i {}:{} y_i \geq 0, i=1,\ldots, n\right\} \\ {}={}& \{A^\intercal y {}:{} y\geq 0\}.\end{aligned}$$

In other words, we take $C$ to be the set of conic combinations (or nonnegative combinations) of the vectors $a_1, \ldots, a_n$.

Next, let us recall from our previous post on support functions (and in particular, Proposition 1.5) that if $K$ is a finitely generated cone, then

$$\begin{aligned}\{A^\intercal y {}:{} y\geq 0\}^{\circ} {}={}& \{x : a_i^\intercal x \leq 0\, i=1,\ldots, p\} \\ {}={}&\{x : Ax \leq 0\}\tag{5a}.\end{aligned}$$

Since $K$ is a convex closed cone, we have $K^{\circ \circ} = K$ [1, Thm 14.5]

$$\{x : Ax \leq 0\}^{\circ} {}={} \{A^\intercal y {}:{} y\geq 0\}. \tag{5b}$$

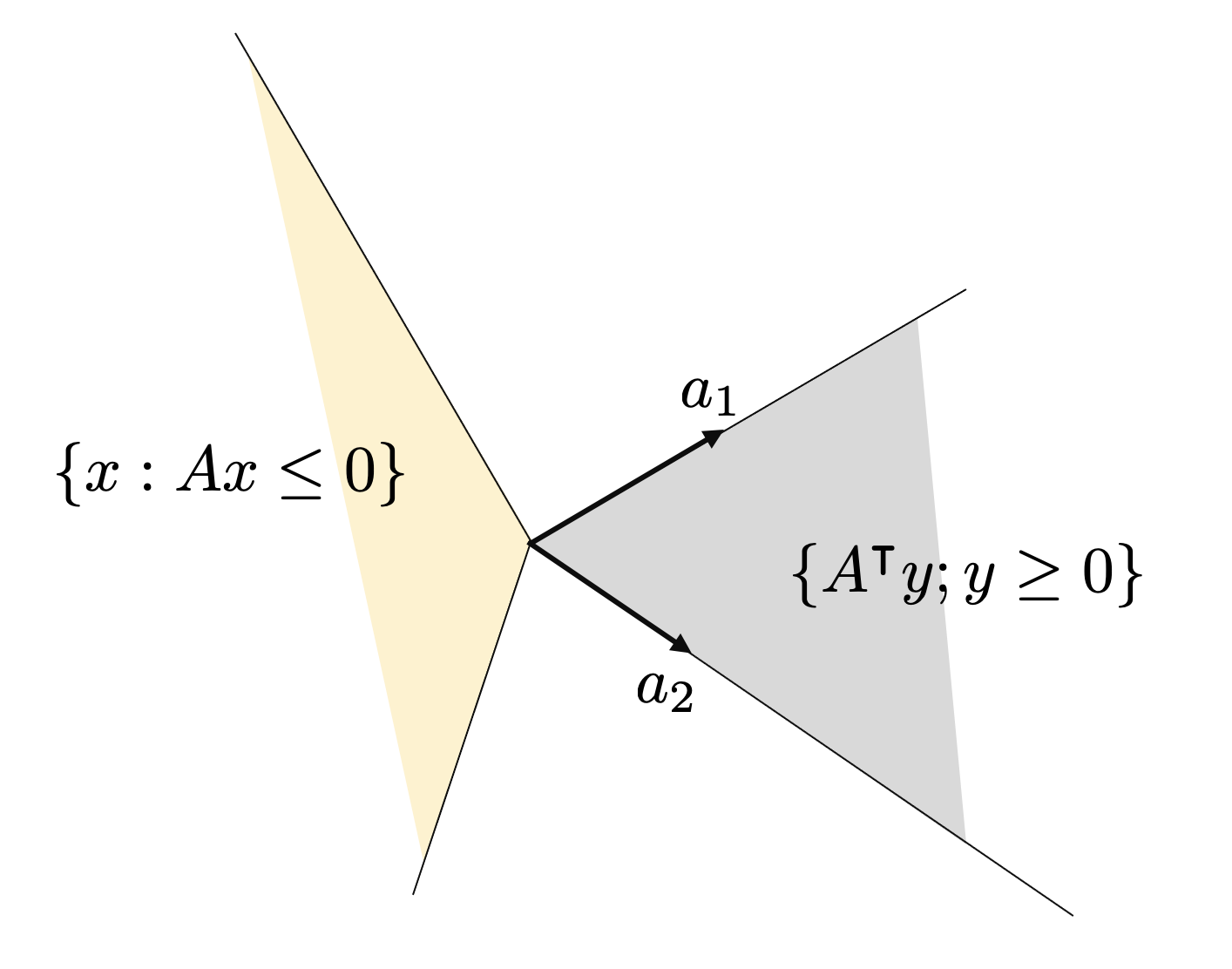
Polar of cone

Figure 0. The polar of $\{x : Ax \leq 0\}$ is the cone $\{A^\intercal y {}:{} y\geq 0\}$ (and vice versa).

Farkas’ lemma

We have actually already proven Farkas' lemma, but let us have a look at its standard formulation:

Lemma 2 (Farkas' lemma). Let $A\in{\rm I\!R}^{m\times n}$ and $b\in{\rm I\!R}^{n}$. Then, exactly one of the following is true

  1. There is $x{}\in{}{\rm I\!R}^{n}$ such that $Ax=b$, $x\geq 0$
  2. There is $y{}\in{}{\rm I\!R}^{m}$ such that $A^\intercal y \geq 0$ and $b^\intercal y < 0$

Let us start by giving a sketch of the proof that will help us gain a geometric understanding of the lemma.

In Figure 1 we see a situation where the second condition of the lemma is satisfied. The light-blue shaded are is the set of all $y$ such that $b^\intercal y < 0$ and the grey shaded cone is the set of $A^\intercal y$ for some $y\geq 0$. We see that the two sets have a nonempty intersection.

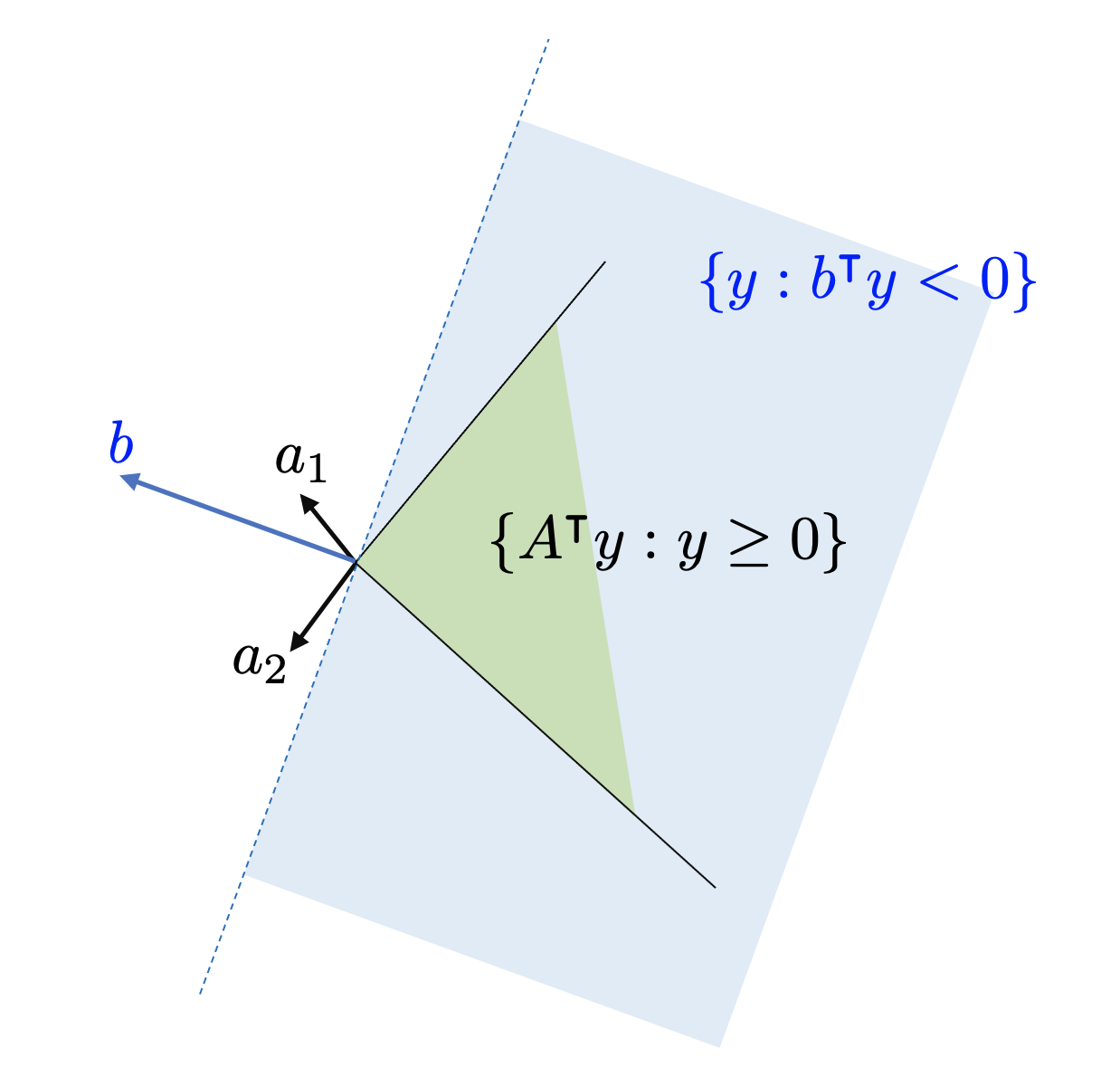
The second condition of Farkas' lemma is satisfied

Figure 1. Condition 2 is satisfied.

In Figure 2 we see a situation where the second condition is not satisfied. In particular, the aforementioned sets are disjoint. As a result, by virtue of the hyperplane separation theorem, we can separate them by a linear function.

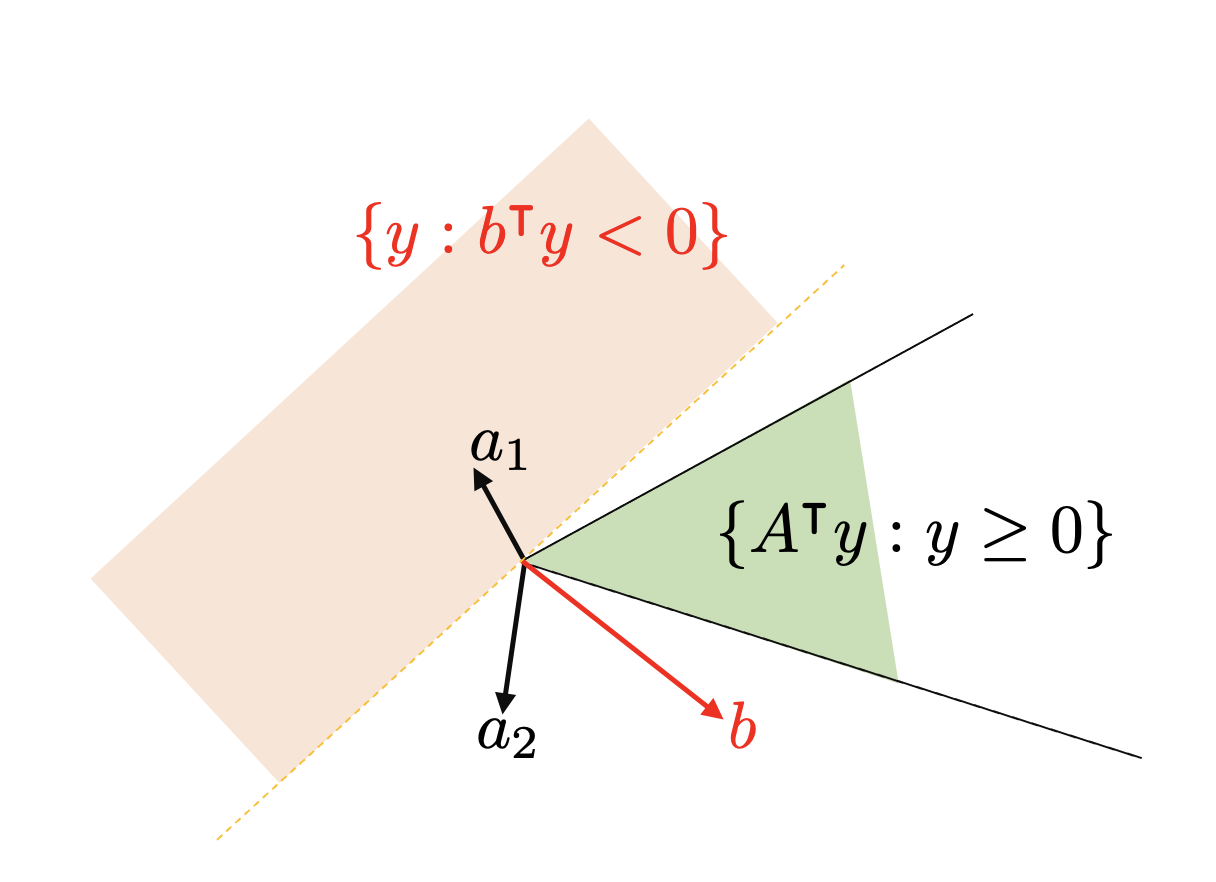
The second condition of Farkas' lemma is not satisfied

Figure 2. Condition 2 is not satisfied.

It remains to see under what conditions the two sets are separated. We will do this in the proof of Farkas' lemma below.

Proof of Farkas' lemma. We start by showing that it is not possible that both conditions are satisfies simultaneously. Suppose instead that both conditions are satisfied. Then, on the one hand

$$y^\intercal A x = y^\intercal b < 0,$$

and on the other hand

$$y^\intercal A x = (A^\intercal y)^\intercal x \geq 0,$$

which is a contradition.

$(1 \Rightarrow \text{not }2).$ We will show that if condition 2 does not hold, then condition 1 holds. Define the sets $K=\{y : A^\intercal y \geq 0\}$ and $L = \{y : b^\intercal y < 0\}$. To say that 2 does not hold is to say that $K$ and $L$ are disjoint. From the hyperplane separation theorem, there is a vector $c$ such that

$$\delta_{K^\circ}(c) \leq -\delta_{(-L)^\circ}(c).$$

This implies that $c \in K^\circ \cap (-L)^\circ$, and the reader can check that this is equivalent to

$$\begin{cases}c = Ax, x \geq 0\\ c = \alpha b, \alpha \geq 0 \end{cases}$$

Implying that $Ax = \alpha b$ with $x\geq 0$ and $\alpha \geq 0$, which is equivalent to $Ax = b$ for some $x\geq 0$ (which is the first condition).

$(2 \Rightarrow 1).$ Likewise. $\blacksquare$

References

  1. R.T. Rockafellar, Convex Analysis, Princeton University Press, 1972