This is a contributed post by NVS Chandra Mouli G.
Introduction
I recently read a paper entitled "A Nonlinear Model Predictive Control Strategy for Autonomous Racing of Scale Vehicles" by Vittorio Cataffo et al., [1] and decided to implement the proposed method in Python3 using OpEn. To study it further, I will be modifying the method to prioritize road safe features over minimum lap time. The purpose of this article is to showcase the formulation and simulation results of an NMPC controlled vehicle system that is road safe (at least in simulations). As a part of experimentation, I will be modifying the approach as the need arises and I will be the updates in future articles accordingly. Going forward, the Telugu letter ttha, ఠ, will be used at the beginning of a section to indicate that a road safety feature is being introduced. Throughout this and the future posts the right-hand coordinate space will be used with the z-axis pointing vertically up, the angles and rotations in counter-clockwise (CCW) direction will be taken as positive. The code used for this post can be found in the Google Colab notebook here.
Software Used
- Python3: An open-source high-level interpreted programming language.
- NumPy: Numerical Python in short NumPy is an open-source scientific computational tool for multidimensional array operations.
- Matplotlib: Is an open-source visualisation library for Python.
- CasADi: Is an open-source tool for nonlinear optimisation and algorithmic (automatic) differentiation.
- Python-control: An open-source control systems library for Python.
- OpEn: Optimization Engine in full, is a framework for designing and solving non-linear and non-convex optimisation problems.
Notation
| Symbol | Expansion | Comment |
|---|---|---|
| $0_{n \times m}$ | $[0]_{n \times m}$ | An $n \times m$ null matrix. |
| $1_{n \times m}$ | $[1]_{n \times m}$ | An $n \times m$ matrix with every element equal to 1. |
| $I_{n}$ | $I_{n \times n}$ | An $n \times n$ identity matrix. |
| $\N$ | $\{0,\ 1,\ 2, \ldots\}$ | Set of all natural numbers. |
| $\N_{[i,\ j]}$ | $\{k \in \N: i \le k \le j\ \forall\ i,\ j \in \N \}$ | Set of all natural numbers between $i$ and $j$ inclusive. |
| $\R$ | $(-\infty,\ \infty)$ | Set of real numbers. |
| $\R^n$ | $\{x_ {n \times 1}: x_i \in \R \ \forall \ i \in \N_{[1,\ n]}\}$ | Set of all $n \times 1$ real vectors. |
| $\R^{n \times m}$ | $\{A_ {n \times m}: a_ {i,\ j} \in \R \ \forall \ i \in \N_{[1,\ n]},\text{ and } j \in \N_{[1,\ m]}\}$ | Set of all $n \times 1$ real vectors. |
| $\R_{[i,\ j]}$ or $[i,\ j]$ | $\{k \in \R: i \le k \le j\ \forall\ i,\ j \in \R\}$ | Set of real numbers from $i$ to $j$ inclusive. |
| $\R_-$ or $\R_{\lt 0}$ | $(-\infty,\ 0)$ | Set of all negative real numbers. |
| $\R_+$ or $\R_{\ge 0}$ | $[0,\ \infty)$ | Set of all positive real numbers. |
| $\mathbb{S}_+^n$ | $\{A\in \R^{n \times n}: x^\mathsf{T}Ax \ge 0 \ \forall \ x \in \R^n \}$ | Set of all symmetric positive semi-definite matrices. |
| $\mathbb{S}_{++}^n$ | $\{A \in \R^{n \times n}: x^\mathsf{T}Ax \gt 0 \text{ and } x^\mathsf{T}Ax = 0 \implies x = 0_n \ \forall \ x \in \R^n \}$ | Set of all symmetric positive definite matrices. |
Section 1: Initial Formulation
This section showcases the simulation results of an NMPC controlled vehicle based on bicycle model dynamics used in [1]. The results in this section are limited to the implementation of vehicle dynamics and the formulation of an NMPC to drive it to a reference position on the global xy-coordinate space. This section does not include autonomous navigation on a track (lane-keeping) and obstacle avoidance, as these will be discussed in a separate post.
The free-body diagram of the bicycle model (inspired by Figure 1 in [1]) is shown in the figure below.
The two-wheel bicycle model in [1] is as follows:
$$\begin{aligned} &\dot{p}_x = v_x \cos{\psi} - v_y \cos{\psi}, \\ &\dot{p}_y = v_x \sin{\psi} + v_y \cos{\psi}, \\ &\dot{\psi} = \omega, \\ &m \dot{v}_x = F_{r, x} - F_{f, y} \sin{\delta} - F_{f, x} \cos{\delta} + m v_y \omega, \\ &m \dot{v}_y = F_{r, y} + F_{f, y} \cos{\delta} + F_{f, x} \sin{\delta} - m v_x \omega, \\ &J_z \dot{\omega} = l_f F_{f, y} \cos{\delta} + l_f F_{f, x} \sin{\delta} - l_r F_{r, y}. \end{aligned}$$
with
$$\begin{aligned} &\alpha_f = - \arctan\left(\frac{\omega l_f + v_y}{v_x}\right) + \delta, \\ &\alpha_r = \arctan\left(\frac{\omega l_r - v_y}{v_x}\right), \\ &F_{f, y} = D_f \sin(C_f \arctan(B_f \alpha_f)), \\ &F_{r, y} = D_r \sin(C_r \arctan(B_r \alpha_r)), \\ &F_{f, x} = F_{r, x} = F_x, \\ &F_x = (C_{m1} - C_{m2} v_x)\tilde{d} - C_{m3} - C_{m4} v^2_x. \end{aligned}$$
Here, $m$ is the mass of the vehicle, $F_{r, x},\ F_{r, y},\ F_{f, x},\text{ and } F_{f, y} \in \R$ are the forces acting on the tires. In the subscript, the letters $r$ and $f$ indicate the rear and front tires, and the letters $x$ and $y$ indicate the longitudinal and lateral component of forces in the local vehicle body xy-frame respectively. The constants $l_f,\text{ and } l_r \in \R_+$ are the distances from the Centre of Gravity $(C_g)$ to front and rear wheels respectively.
The control inputs $\tilde{d} \in [0, 1],\text{ and } \delta \in \R$ are the normalised forward acceleration PWM duty cycle of the electric drive train motor [2] and front wheel steering angle input in radians respectively. The states $p_x,\ p_y,\text{ and } \psi \in \R$ are the vehicle's x position in meters, the y position in meters, and the heading in radians in the global frame of reference respectively. The states $v_x$, $v_y$, and $\omega \in \R$ are the vehicle's x velocity in meters-per-second, the y velocity in meters-per-second, and the angular rotation rate around the z-axis in radians-per-second in the local body-fixed frame of reference respectively.
The constants $B_f$, and $B_r \in \R$ are the stiffness factors, $C_f$, and $C_r \in \R$ are the shape factors $D_f$, and $D_r \in \R$ are the peak factors, and $C_{m1}$, $C_{m2}$, $C_{m3}$, and $C_{m4} \in \R_+$ are empirical parameters as described in [1]. The parameters $\alpha_f$ and $\alpha_r$ are the slip angles. These equations and their parameters are described in equations (1) through (4) in [1]. Now the dynamics can be written as,
$$\dot{z}_t = \mathbf{g}(z_t,\ u_t).$$
with
$$ \begin{aligned} &z_t = [p_x(t),\ p_y(t),\ \psi(t),\ v_x(t),\ v_y(t),\ \omega(t)]^\mathsf{T}, \\ &u_t = [\tilde{d}(t),\ \delta(t)]^\mathsf{T}, \\ &\mathbf{g} : \R^{n_x} \times \R^{n_u} \rightarrow \R^{n_x}, \\ &n_x = 6 \text{ and } n_u = 2. \end{aligned}$$
Here, $z_t$ is the state vector and $u_t$ is the input vector. Using forward Euler method, the discretised system for some small sampling time $T >0$ can be written as,
$$ z_{k + 1} = z_k + T \cdot \mathbf{g}(z_k, u_k), \ k \in \N. $$
Throughout this article, the vehicle parameters are taken as described in Table 1 in [1]. They are given (estimated) as,
| Param | Value | Param | Value | Param | value |
|---|---|---|---|---|---|
| $l_f$ | $0.178$ m | $l_r$ | $0.147$ m | $m$ | $5.6292$ kg |
| $J_z$ | $0.204$ kg m$^2$ | $B_f$ | $9.242$ | $B_r$ | $17.716$ |
| $C_f$ | $0.085$ | $C_r$ | $0.133$ | $D_f$ | $134.585$ N |
| $D_r$ | $159.919$ N | $C_{m1}$ | $20$ N | $C_{m2}$ | $6.92 \cdot 10^{-7}$ kg s$^{-1}$ |
| $C_{m3}$ | $3.99$ N | $C_{m4}$ | $0.67$ kg m$^{-1}$ | $M$ | $1674$ |
The following code snippet shows the definition of constants of the bicycle dynamics in Python3.
# Definition of constants
Ts = 0.01
car_width = 0.25
car_length = 0.4
nz = 6
nu = 2
m = 5.692
Jz = .204
lf = .178
lr = .147
Bf = 9.242
Br = 17.716
Cf = .085
Cr = .133
Df = 134.585
Dr = 159.919
Cm1 = 20
Cm2 = 6.92E-7
Cm3 = 3.99
Cm4 = .67
The bicycle dynamics are defined in Python3, as follows:
import casadi as cs
# Bicycle dynamics function
def dynamics(z, u):
xt = z[0]
yt = z[1]
psi_t = z[2]
vxt = z[3]
vyt = z[4]
omega_t = z[5]
pwm_t = u[0]
delta_t = u[1]
alpha_f = -cs.atan2(omega_t*lf + vyt, vxt) + delta_t
alpha_r = cs.atan2(omega_t*lr - vyt, vxt)
Ffy = Df*cs.sin(Cf*cs.atan2(Bf*alpha_f, 1))
Fry = Dr*cs.sin(Cr*cs.atan2(Br*alpha_r, 1))
Frx = (Cm1 - Cm2*vxt)*pwm_t - Cm3 - Cm4*vxt**2
Ffx = Frx
xt = xt + Ts*(vxt*cs.cos(psi_t) - vyt*cs.sin(psi_t))
yt = yt + Ts*(vxt*cs.sin(psi_t) + vyt*cs.cos(psi_t))
psi_t = psi_t + Ts*omega_t
vxt = vxt + Ts*(Frx - Ffy*cs.sin(delta_t) + Ffx*cs.cos(delta_t) + m*vyt*omega_t)/m
vyt = vyt + Ts*(Fry + Ffy*cs.cos(delta_t) + Ffx*cs.sin(delta_t) - m*vxt*omega_t)/m
omega_t = omega_t + Ts*(lf*Ffy*cs.cos(delta_t) + lf*Ffx*cs.sin(delta_t) - lr*Fry)/Jz
return cs.vertcat(xt, yt, psi_t, vxt, vyt, omega_t)
The goal is to formulate an NMPC that minimises the distance between the desired final position $p^d = [p_x^d,\ p_y^d]^\mathsf{T}$ and the position of the vehicle $p_N = [p_x^N,\ p_y^N]^\mathsf{T}$ after $N$ (prediction horizon) time steps. This can also be interpreted as asking the MPC controller to take the system as close as possible to the desired final position with in a given time of $N \cdot T$ seconds. Whilst doing so, the controller shall ensure that the system obeys the state and input (safety) constraints, given as:
$$ \begin{aligned} &v_x \in \bm{\Gamma} = [0,\ 5], \\ &\begin{bmatrix} \ \tilde{d} \ \\ \ \delta \ \end{bmatrix} \in \mathbf{U} = [0,\ 1] \times \left[-\frac{\pi}{3},\ \frac{\pi}{3}\right]. \end{aligned} $$
It should also be of priority that the system is not subjected to violently arbitrary accelerations and steering angles. This can be formulated as aiming for a minimum jerk trajectory and can be modelled as minimising the distance between successive input vectors. With this, the NMPC formulation takes the following form,
$$ \begin{aligned} \mathbb{P}_ N(z, u^\star_ {\text{p}}) :\ &\underset{\bm{u}_ N}{\text{minimise}}\ \|p_ N - p^d\|_ {Q_ {1}}^2 + \sum_ {k=0}^{N-1} \|u_ k - u_ {k-1}\|_ {Q_ 2}^2 \\ \text{s.t.}\ & z = z^\star_ {\text{p}}, \\ \ &u_ {-1} = u^\star_ {\text{p}}, \\ \ &z_ {k+1} = \mathbf{g}(z_ k, u_ k),\ k \in \N_ {[0, N-1]}, \\ \ &u_ k \in \mathbf{U},\ k \in \N_ {[0, N-1]}, \text{ and} \\ \ &v_ {x, k} \in \bm{\Gamma},\ k \in \N_ {[0, N-1]}. \end{aligned} $$
Note: The control input $u^\star_{\text{p}}$ is the control input used to drive the vehicle during the previous iteration resulting in the state $z^\star_ p$. For the first iteration the control input $u_ {-1}$ is the input that the system began with i.e., the input at $t=-T$.
Here, $Q_ 1 \in \mathbb{S}^{2}_ {++}$ and $Q_ 2 \in \mathbb{S}^{n_ u}_ {++}$. The minimisation problem $\mathbb{P}_ N$ is solved at every time step in a loop. The set of all possible minimisers of $\mathbb{P}_ N$ is denoted as $\mathcal{U}_ N^\star(z, u^\star_ {\text{p}})$ where,
$$\mathcal{U}_N^\star(z, u^\star_{\text{p}}) = \underset{\bm{u}_ N}{\text{argmin}} \left\{ \begin{aligned} &\|p_N - p^d\|_{Q_{1}}^2 + \\ &\sum_{k=0}^{N-1} \|u_k - u_ {k-1}\|_{Q_2}^2 \end{aligned} \middle| \begin{aligned} & z_ 0 = z^\star_ {\text{p}},\ u_ {-1} = u^\star_{\text{p}}, \\ \ &z_ {k+1} = \mathbf{g}(z_k, u_k), \\ \ &u_k \in \mathbf{U}, \text{ and } v_{x, k} \in \bm{\Gamma}, \\ \ &\forall \ k \in \N_{[0, N-1]}. \end{aligned} \right\}$$
The NMPC algorithm is as follows:
With, $u_ {-1} = 0_ {n_ u\times 1}$ and $z$ as the initial state, for iteration $i=0$ at time $t=0$ compute $\bm{u}_ N^\star(z, u^\star_ {\text{p}}) \in \mathcal{U}_ N^\star(z, u^\star_ {\text{p}})$ by solving $\mathbb{P}_ N$. Then, take the first computed optimal control input $u^\star(z, u^\star_{\text{p}})$ and apply it to the system.
Now, take a measurement of the resulting state $z^\star_ {1}$. With $u_ {-1} = u^\star(z, u^\star_ {\text{p}})$ and $z = z^\star_ 1$, proceed to iteration $i=1$ at $t=T$ to solve $\mathbb{P}_ N$ again. Obtain the new optimal control input $u^\star$ and apply it to the system.
Take a new measurement of the resulting state $z^\star_ 1$ and move on to iteration $i=2$ at $t = 2T$. This procedure is repeated indefinitely or till a set number of iterations is reached. Throughout this article the total number of simulation steps (iterations) is denoted by $S$.
Note: The reader might notice that this iterative method only works assuming that the computation of $\bm{u}_N^\star$ takes less than $T$ seconds during each iteration. It is indeed the case and it is not clear what happens if each computation takes longer than $T$ seconds. This hurts the confidence on the designed system, as it might produce unexpected results. Thus, the selection of $T$ shall be of careful consideration owing to the trade off between the accuracy of the discrete approximation and computational limitations.
The following code snippet shows the definition of the NMPC parameters and constants in Python3.
import numpy as np
import opengen as og
import casadi.casadi as cs
nz = 6 # Number of states
nu = 2 # Number of inputs
N = 50 # Prediction horizon
vmin = 0 # Minimum value of vx
vmax = 5 # Maximum value of vx
umin_seq = [0, -np.pi/3] * N # Minimum value of inputs
umax_seq = [1, np.pi/3] * N # Maximum value of inputs
Q1 = np.diagflat([10000, 10000, 0, 0, 0, 0]) # Weight matrix Q1
Q2 = np.diagflat([1, 5]) # Weight matrix Q2
u_seq = cs.SX.sym("u_seq", N * nu, 1)
problem_params = cs.SX.sym("problem_params", 2*nz + nu, 1)
# [z, z_d, u_{-1}]
z = problem_params[ : nz] # Initial state
z_d = problem_params[nz : 2 * nz] # Reference (destination) state
u_prev = problem_params[2 * nz : 2 * nz + nu] # u_{-1} value of inputs at t=-Ts
z_t = z # Start with current state as initial state
total_cost = 0
penality_constraint_vx = 0
# Define the stage cost
def stage_cost(u_current, u_prev):
return (u_current.T - u_prev.T) @ Q2 @ (u_current - u_prev)
# Define the terminal cost
def terminal_cost(z):
return (z.T - z_d.T) @ Q1 @ (z - z_d)
The formulation of on the NMPC in Python3 is shown in the code snippet below.
# Formulate the NMPC total cost and constraints
for t in range(N):
u_current = u_seq[t * nu : (t + 1) * nu] # Set current time step input
total_cost += stage_cost(u_current, u_prev) # Add stage cost to total cost for the current time step
z_t = dynamics(z_t, u_current) # Set current state to resultant state of the current input
u_prev = u_current # Change previous input to current input for next iteration
penality_constraint_vx += cs.fmax(0, cs.norm_1(z_t[3]) - vmax) # Add set vx maximum constraint
penality_constraint_vx += cs.norm_1(cs.fmin(vmin, z_t[3])) # Add set vx minimum constraint
# Add terminal cost to total cost
total_cost += terminal_cost(z_t)
# Define rectangular constraints for inputs
U = og.constraints.Rectangle(umin_seq, umax_seq)
# Define and build the problem
problem = og.builder.Problem(u_seq, problem_params, total_cost)
problem = problem.with_constraints(U)
problem = problem.with_penalty_constraints(penality_constraint_vx)
build_config = og.config.BuildConfiguration() \
.with_build_directory("optimizer") \
.with_tcp_interface_config()
meta = og.config.OptimizerMeta().with_optimizer_name("bicycle_model")
solver_config = og.config.SolverConfiguration()\
.with_tolerance(1e-4)\
.with_penalty_weight_update_factor(3)
builder = []
builder = og.builder.OpEnOptimizerBuilder(problem, meta,
build_config, solver_config).with_verbosity_level(0)
builder.build()
This setup is implemented and simulated in Python3 with $N=50,\ S = 300,\ T=0.01 \text{ s},\ z = 0_{n_x \times 1} \text{ and }p^ d = [5, 5]^\mathsf{T}$ and the following code snippet shows the implementation.
import numpy as np
import opengen as og
# Define the TCP server manager
mng = og.tcp.OptimizerTcpManager("optimizer/bicycle_model")
# Start the TCP server
mng.start()
# Simulation config
simulation_steps = 300
# Simulations parameters
current_position = [0, 0] # p
pos_ref = [5, 5] # p^d
z_state_0 = np.array([*current_position, 0, 0, 0, 0]).reshape(nz, 1) # z
z_ref = np.array([*pos_ref, 0, 0, 0, 0]).reshape(nz, 1) # z^d
u_prev = np.array([0, 0]).reshape(nu, 1) # Previous input at t=-Ts
# Matrices to record states and inputs during simulation, for plotting
state_sequence = np.zeros((simulation_steps, nz)) # Matrix to record states
input_sequence = np.zeros((simulation_steps, nu)) # Matrix to record inouts
state_sequence[0, :] = np.array(z_state_0.reshape(nz)) # Set initial states
z_current = z_state_0 # Set current state to initial state
for k in range(simulation_steps-1):
# Set problem parameters
solver_response = mng.call(p=[*z_current.flatten(), *z_ref.flatten(), *u_prev.flatten()])
# Check if solver failed
if not solver_response.is_ok():
out = solver_response.get()
print(f"solver failed! with exit code: {out.code}")
print(f"and message: {out.message}")
print(f"at time step = {k}")
break
out = solver_response.get() # Get response
us = out.solution # Get the input solution sequence
u_mpc = us[0:nu] # Only use the first computed input
# Simulate and get next state using the computed input
z_next = np.array(dynamics(z_current, u_mpc)) # Set next state
u_prev = np.array(u_mpc) # Make current input as previous input
state_sequence[k+1, :] = z_next.T # Update the states record
input_sequence[k, :] = u_mpc # Update the inputs record
z_current = z_next.flatten() # Set the current state to next state
# Make sure to kill the serve when the simulation is over
mng.kill()
The simulation results are shown in the following GIF.
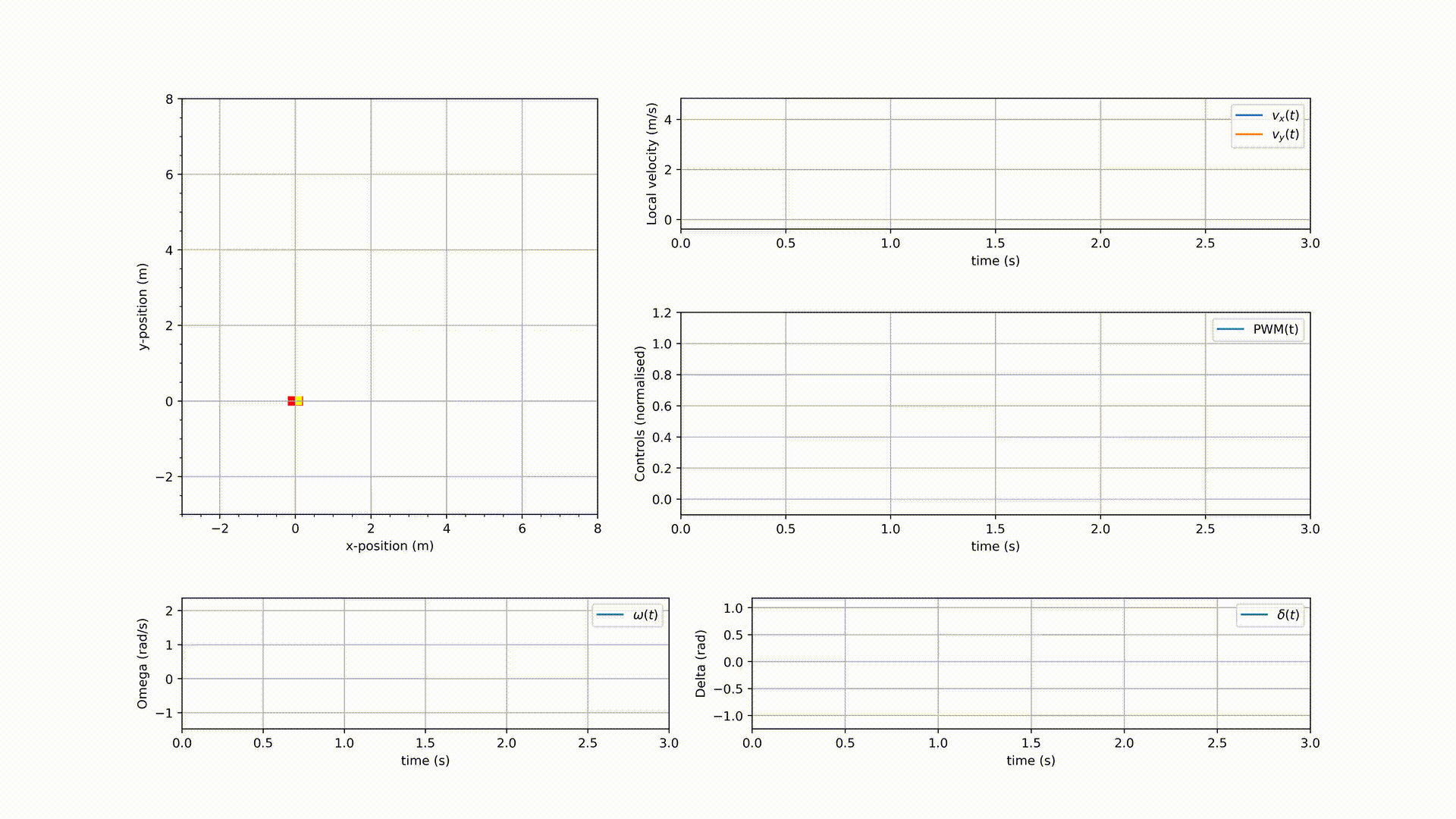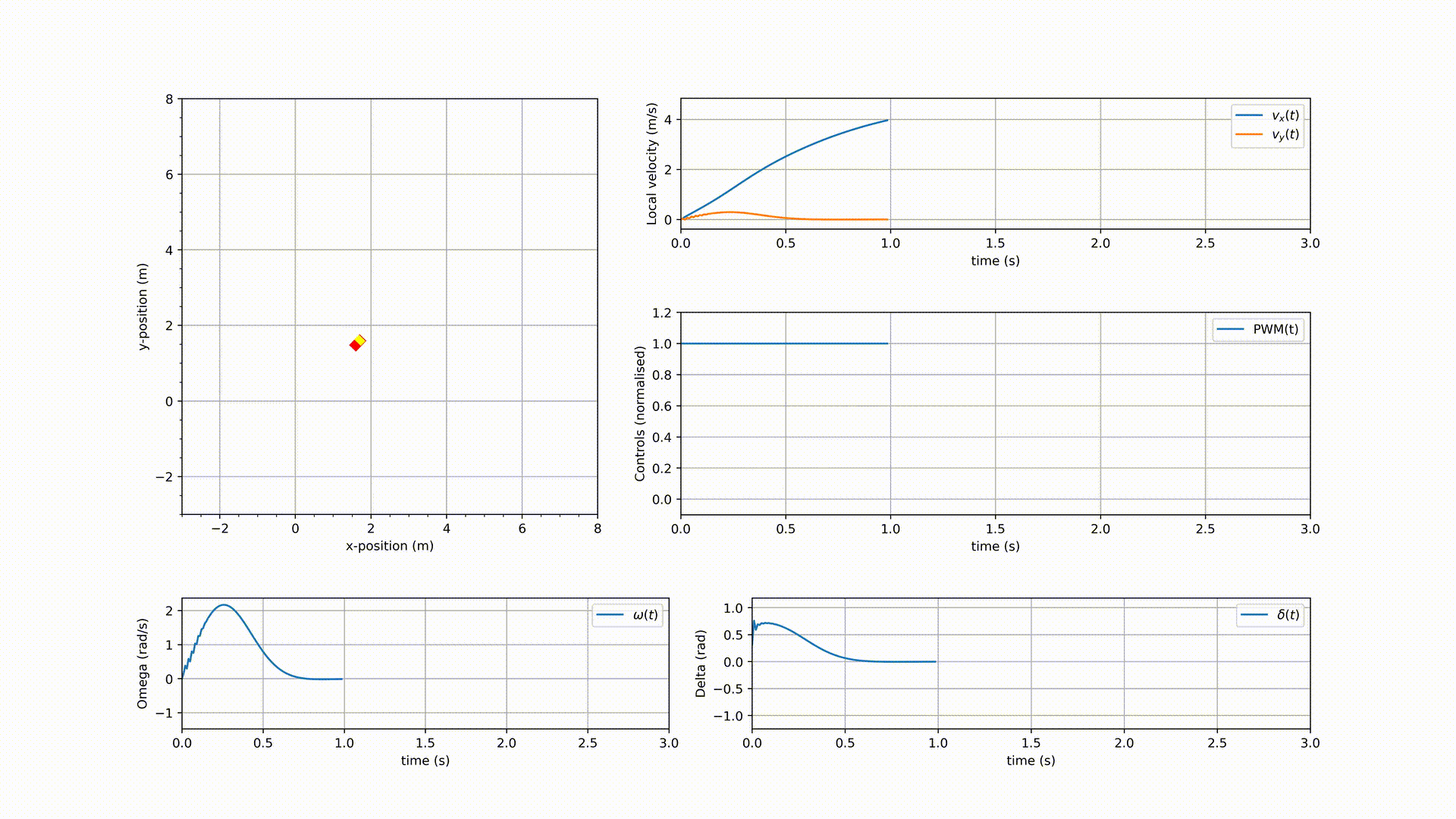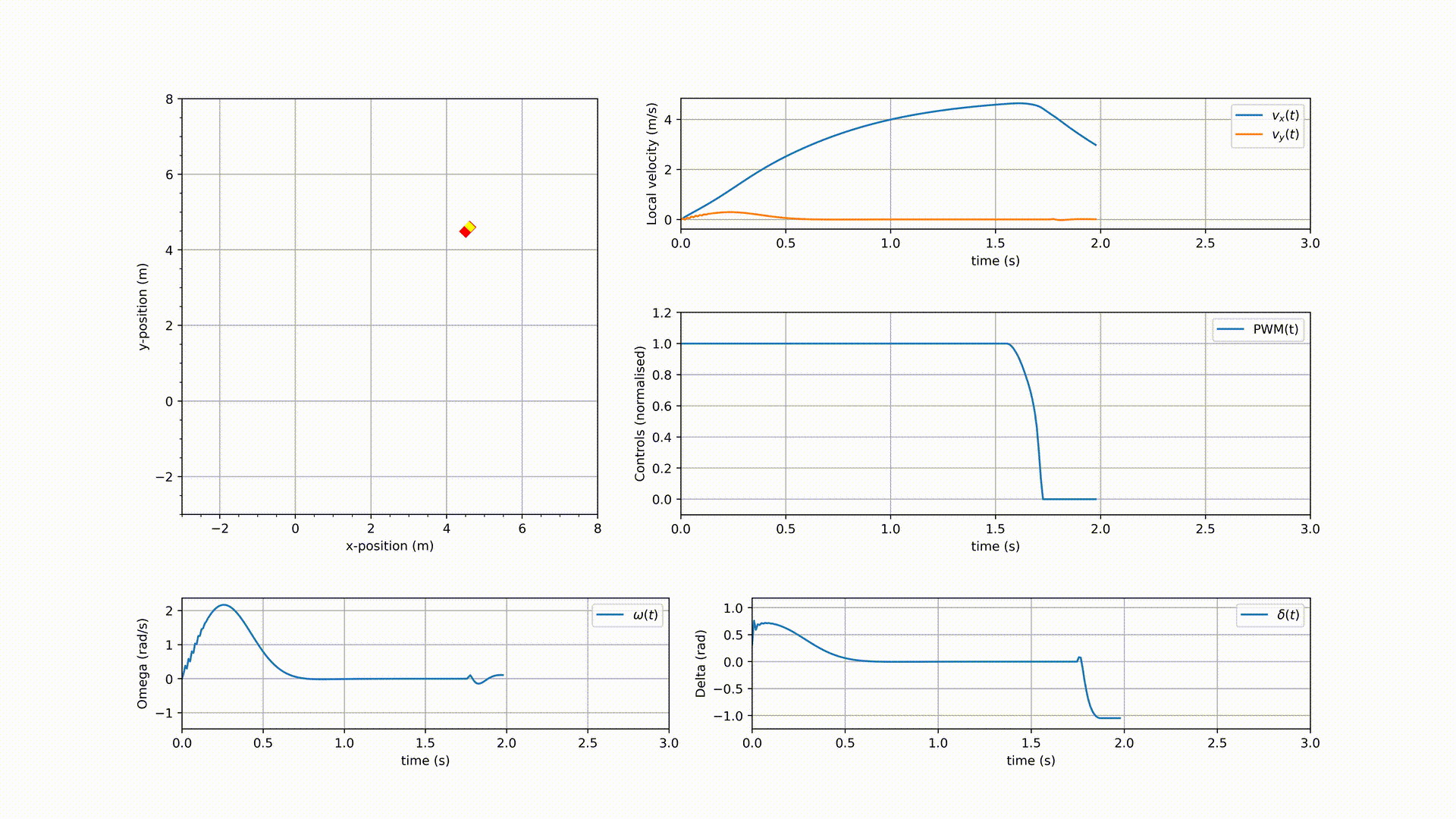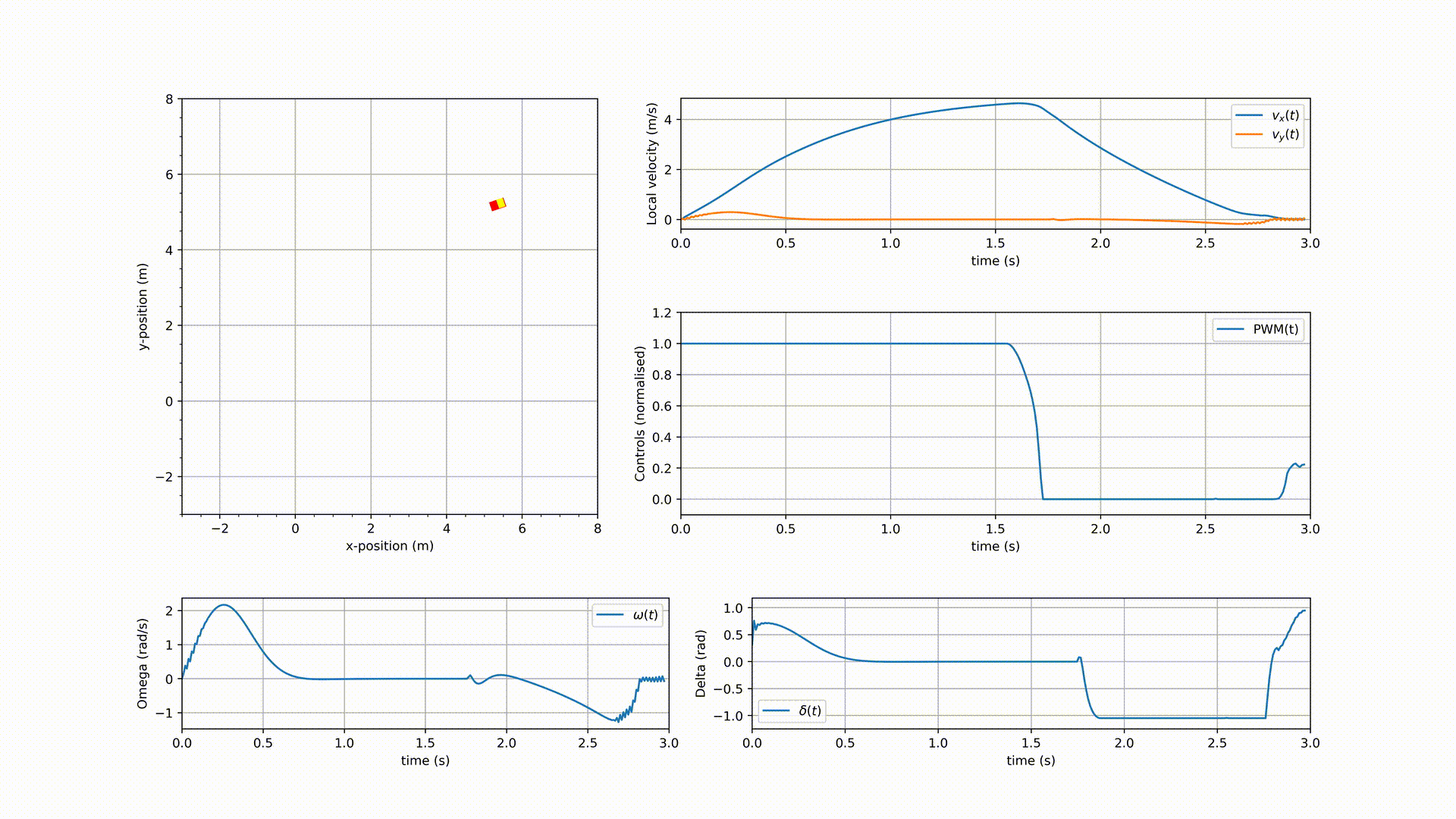
As it can be seen in the GIF, the NMPC controlled vehicle indeed drove towards (close to) the destination $[5, 5]^\mathsf{T}$, but it didn’t converge. It could have been a matter of tuning $Q_1$ and $Q_2$, but before tuning them, the vehicle dynamics need to be modified to add a braking system. Remember, the end goal is to have an NMPC controlled autonomous vehicle that is road safe. These preliminary results are good enough for now as the weight matrices $Q_1$ and $Q_2$ might need retuning when the dynamics have changed.
ఠ Section 2: Let’s brake (or rather not)
This section discusses the addition of a braking system to the vehicle dynamics. The dynamics shall be modified with caution, as it might make the system uncontrollable. In the end, a simulation result is provided for the modified system under the same scenario as in Section 1.
In the equation of $F_x$ in the dynamics, the term $C_{m3}$ might be acting as the initial resistance of static friction between the tires and the road, while the term $C_{m4}v^2_x$ acts as the force due to air drag as the vehicle starts to move. Though, this captures the initial and forward moving dynamics, this model only accurate when $\tilde{d} > 0$.
Leaving $\tilde{d} = 0$, then at $t=0$, $F_x = -C_{m3}$, which makes $v_x < 0$. Since, $v_x^2 > 0$, the negative x-force on the vehicle increases quadratically as $F_x = -C_{m3} - C_{m3}v_x^2$. Also, when the vehicle starts moving i.e., $|v_x| > 0$, the term $C_{m3}$ should vanish, or should switch to rolling fictional force between the tires and the road. It would also make sense to make $\text{sign}(C_{m4}) = \text{sign}(v_x)$ to properly model air drag. These will require additional modifications in the dynamics that might require conditional expressions, which are currently not supported by OpEN. Nonetheless, this inaccuracy should be kept in mind when interpreting the simulation results.
Due to the above reasons, moving forward it is assumed that the simulation results are valid as long as $\tilde{d} > 0$ and $v_x > 0$ (this excludes the lower bound of $v_x$ in the above formulation) and any part of the simulation that violates these conditions (even when $v_x = 0$) shall be considered inaccurate. This also means that, going forward $C_{m3}$ is assumed to be the rolling frictional force between the tires and the road.
With these conditions under consideration, the addition of the braking system can be done by the following modifications to the system dynamics,
$$ \begin{aligned} &F_\text{brake} = \mu_{KF}\tilde{b}, \\ &\tilde{b} \in [0, 1], \\ &\mu_{KF} > 0, \\ &F_x = (C_{m1} - C_{m2} v_x)\tilde{d} - C_{m3} - C_{m4} v^2_x - F_\text{brake}. \end{aligned}$$
Here, $\mu_{KF}$ is a constant that relates the normalised brake input $\tilde{b}$ and the actual braking force $F_\text{brake}$, and not exactly equal to the coefficient of kinetic friction. From here on the value of $\mu_{KF}$ is assumed to be $0.1$. It should be noted that the sign of $F_\text{brake}$ is only valid if $v_x > 0$.
The brake constant is define in Python3 as follows:
nu = 3 # Change number of inputs to 3
# Definition of brake constant
brake_constant = 0.1
umin_seq = [0, -np.pi/3, 0] * N # Minimum value of inputs
umax_seq = [1, np.pi/3, 1] * N # Maximum value of inputs
The following code snippet shows the modified bicycle dynamics in python.
import casadi as cs
# Bicycle dynamics function
def dynamics(z, u):
xt = z[0]
yt = z[1]
psi_t = z[2]
vxt = z[3]
vyt = z[4]
omega_t = z[5]
pwm_t = u[0]
delta_t = u[1]
brake = u[2] # Addition of brake input
alpha_f = -cs.atan2(omega_t*lf + vyt, vxt) + delta_t
alpha_r = cs.atan2(omega_t*lr - vyt, vxt)
Ffy = Df*cs.sin(Cf*cs.atan2(Bf*alpha_f, 1))
Fry = Dr*cs.sin(Cr*cs.atan2(Br*alpha_r, 1))
Frx = (Cm1 - Cm2*vxt)*pwm_t - Cm3 - Cm4*vxt**2
Ffx = Frx
xt = xt + Ts*(vxt*cs.cos(psi_t) - vyt*cs.sin(psi_t))
yt = yt + Ts*(vxt*cs.sin(psi_t) + vyt*cs.cos(psi_t))
psi_t = psi_t + Ts*omega_t
Fx_brake = brake_coeff_of_kinetic_fric * brake # Compute the brake force
# Subtrack brake force from Fx
vxt = vxt + Ts*(Frx - Fx_brake - Ffy*cs.sin(delta_t) + (Ffx - Fx_brake)*cs.cos(delta_t) + m*vyt*omega_t)/m
vyt = vyt + Ts*(Fry + Ffy*cs.cos(delta_t) + (Ffx - Fx_brake)*cs.sin(delta_t) - m*vxt*omega_t)/m
omega_t = omega_t + Ts*(lf*Ffy*cs.cos(delta_t) + lf*(Ffx - Fx_brake)*cs.sin(delta_t) - lr*Fry)/Jz
return cs.vertcat(xt, yt, psi_t, vxt, vyt, omega_t)
With these modifications to the dynamics, starting from $z = 0_{n_x \times 1}$, the modified system is simulated in Python3 with $N=50,\ S = 300,\ T=0.01, \text{ and } p^d = [5, 5]^\mathsf{T}$ and the results are shown in the following GIF.
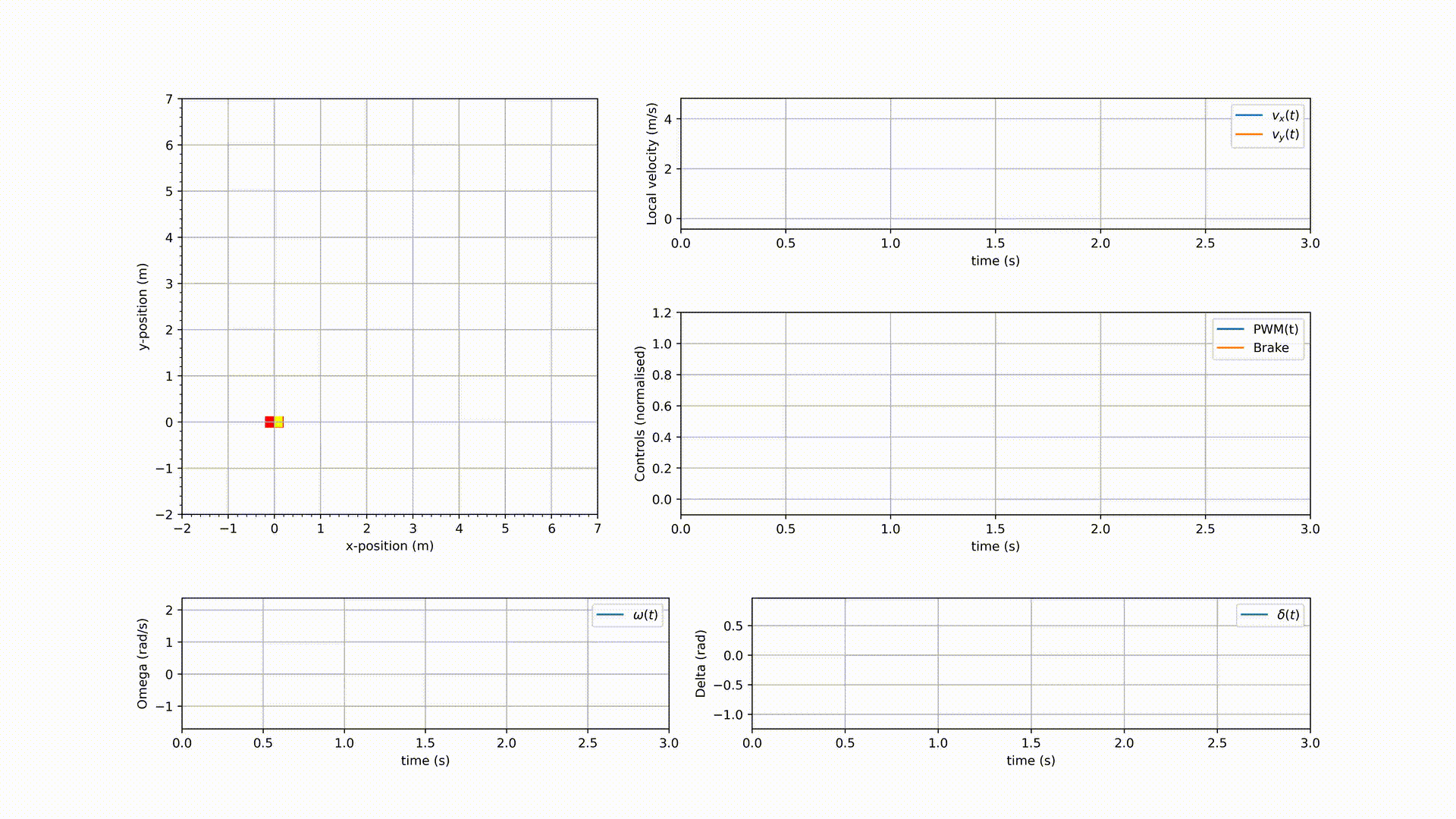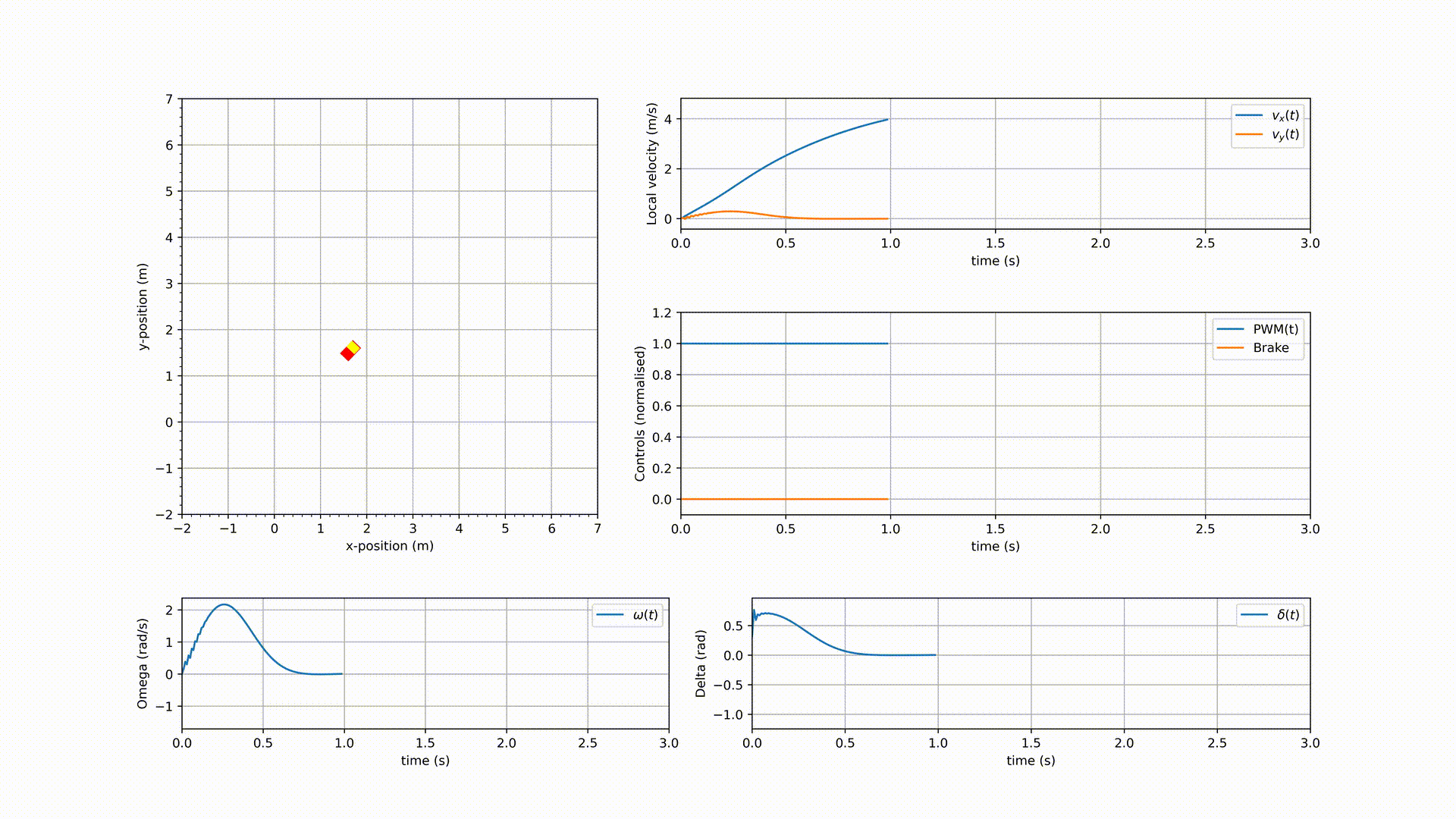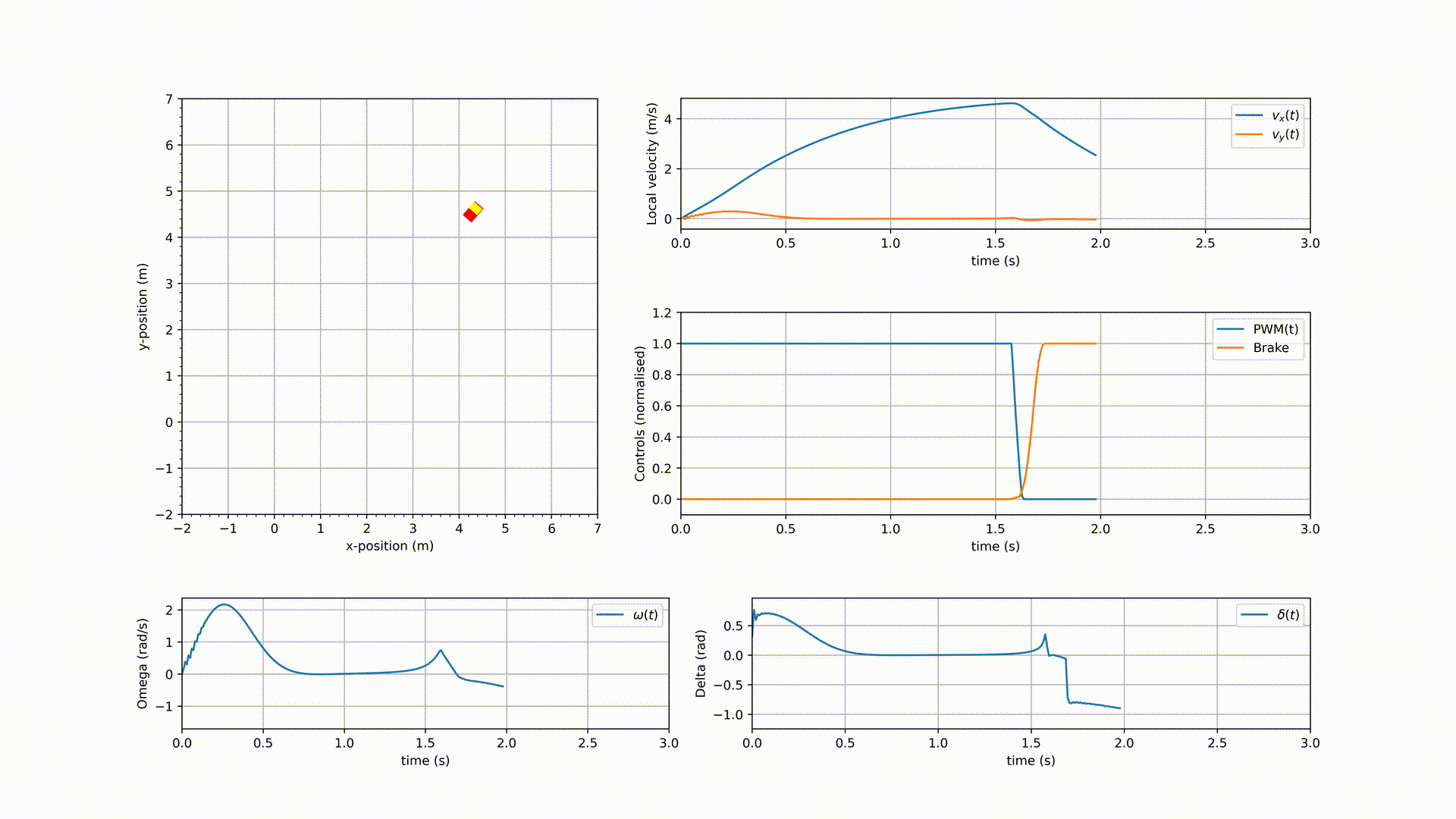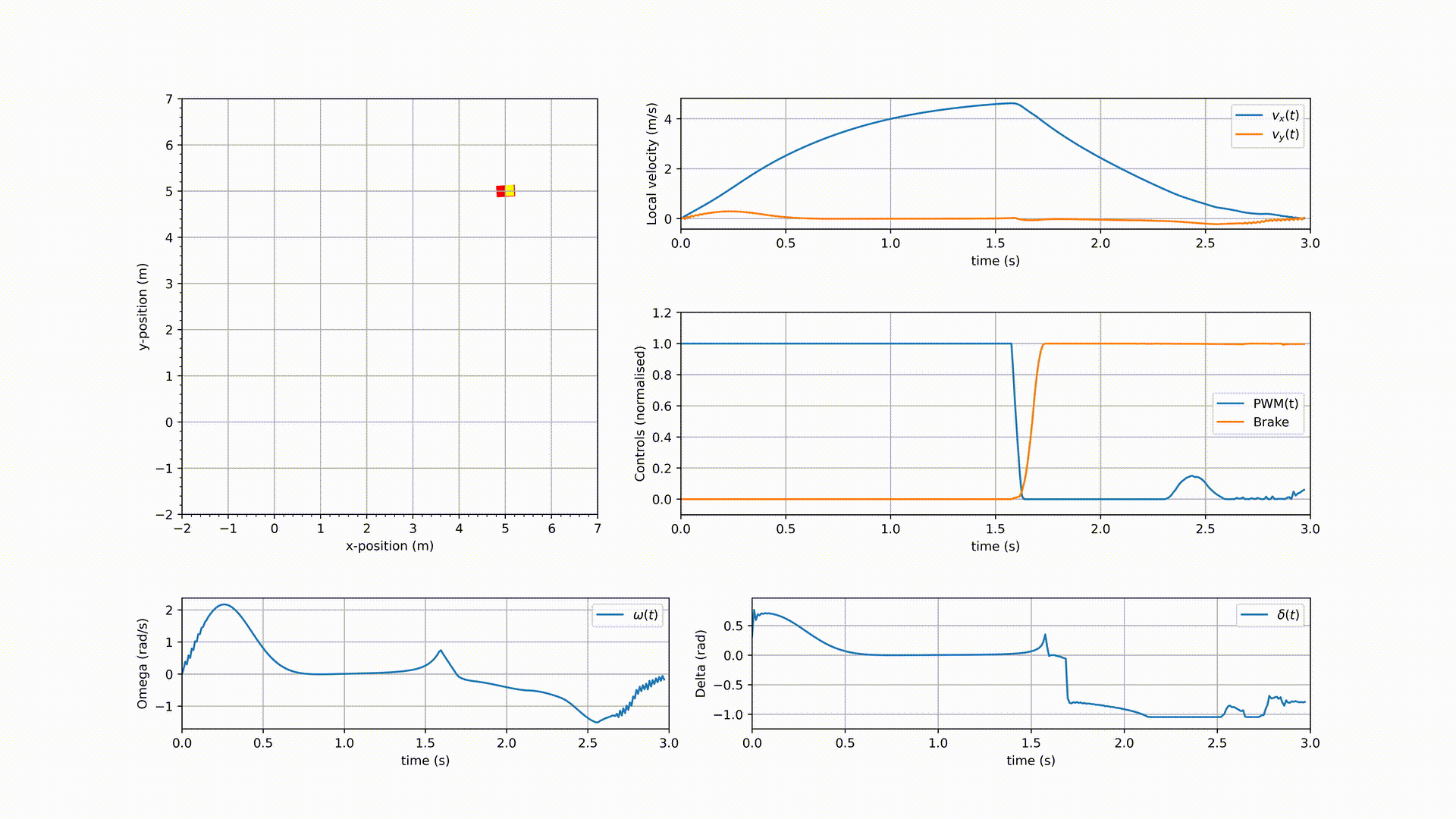
As it can be seen from the results, indeed the vehicle reaches close to $z^d = [5, 5, 0, 0, 0, 0]^\mathsf{T}$ i.e., $p^d = [5, 5]^\mathsf{T}$. While this is a good result, it should also be noted that between $t=2.25$ and $t=2.5$, the controller is applying acceleration PWM $(\tilde{d})$ and brake input $(\tilde{b})$ simultaneously. The fix for this undesirable usage of $\tilde{d}$ and $\tilde{b}$, and the addition of lane-keeping and obstacle avoidance will be discussed in a future article.
References
- Cataffo, Vittorio & Silano, Giuseppe & Iannelli, Luigi & Puig, Vicenç & Glielmo, Luigi. (2022). A Nonlinear Model Predictive Control Strategy for Autonomous Racing of Scale Vehicles. 10.1109/SMC53654.2022.9945279.
- Liniger, A., Domahidi, A., & Morari, M. (2017). Optimization-Based Autonomous Racing of 1:43 Scale RC Cars. Available at https://doi.org/10.1002/oca.2123.
Acknowledgements: I would like to thank and acknowledge Dr. Pantelis Sopasakis for his valuable suggestions and insights during the proof reading of this article. I would also like to thank him for hosting this article.
About the author
My name is Chandra Mouli G, I am a top-graduating MSc Electronics student from the Queen’s University Belfast, with a strong academic foundation in Electrical and Electronics Engineering (B.Tech. E.E.E). For my MSc final project, I developed an altitude control system for drones using a Kalman Filter and a linear multivariate controller. I recently co-authored a paper on "An Open-Source Quadcopter for Wind Field Surveying” (link) featuring my altitude control algorithm and I also have three other AI-related publications.
My career interests are autonomous robotics, and advanced control engineering. I am particularly focused on the fields of nonlinear and linear optimal control, model predictive control, stochastic systems and estimation, and reinforcement learning.
My technical skillset includes Control engineering, Embedded Systems, AI and Machine Learning, analog and digital electronics design and analysis. I am proficient in C++, Java, Python3, and MATLAB.