Here we study the problem of projecting onto the epigraph of a convex continuous function. Unlike the computation of the proximal operator of a function or the projection on its sublevel sets, the projection onto epigraphs is more complex and there exist only a few functions for which semi-explicit formulas are available.
KKT Optimality Conditions
Let $f:{\rm I\!R}^n\to{\rm I\!R}\cup\{\infty\}$ be a proper, convex, continuous function; its epigraph is the nonemtpy convex closed set
$$ \begin{aligned} \mathrm{epi} f := \{(x,t) \in {\rm I\!R}^n\times {\rm I\!R} {}\mid{} f(x) \leq t \}. \end{aligned} $$
For convenience, we define the projection of a pair $ (x, t)\in{\rm I\!R}^n\times {\rm I\!R}$ onto the epigraph of $ f$ as
$$\begin{aligned} \Pi_f(x, t) := \mathrm{proj}_{\mathrm{epi} f}(x, t). \end{aligned}$$
Let $ (x, t)\in{\rm I\!R}^n\times {\rm I\!R}$. If $ (x, t)\in\mathrm{epi} f$, then $\Pi_f(x, t) = (x, t)$.
Suppose $(x, t)\notin\mathrm{epi} f$. Let $x^{\star}=x^{\star}(x, t)$ and $t^{\star}=t^{\star}(x, t)$ so that $\Pi_f(x, t)=(x^{\star}, t^{\star})$.
Proposition 1 (Optimality conditions). Let $f:{\rm I\!R}^n\to{\rm I\!R}\cup\{\infty\}$ be a proper, convex, continuous function. For a given $(x, t) \notin \mathrm{epi} f$, we have that $\Pi_f(x,t)=(x^{\star}, t^{\star})$ if and only if
$$\begin{aligned}x - x^{\star} {}\in{} (f(x^{\star})-t) \partial f(x^{\star}),\tag{1}\end{aligned}$$
and $f(x^{\star}) {}={} t^{\star}.$
It might be necessary to employ numerical methods to solve the optimality conditions.
Dual epigraphical projection
Proposition 2 (Dual problem). The dual problem is
$$ \begin{aligned} \operatorname*{Maximize}_{y\geq 0}\ q(y) \coloneqq y (f^y(x) - \tfrac{y}{2} -t), \end{aligned}$$
where $f^y$ is the Moreau envelope of $f$ with parameter $y$.
Consider again the optimization problem ${\rm I\!P}(x, t)$ which defines the epigraphical projection. We introduce the Lagrangian
$$ \begin{aligned} \mathcal{L}(\chi,\tau, y) = \tfrac{1}{2}\|\chi - x\|^2 + \tfrac{1}{2}(\tau - t)^2 + y(f(x)-\tau). \end{aligned}$$
We compute the partial subdifferentials of $\mathcal{L}$ with respect to the primal variables $ (\chi, \tau)$:
$$ \begin{aligned} \partial_{\chi}\mathcal{L}(\chi, \tau, y) &= \chi - x + y\partial f(x),\\ \partial_{\tau}\mathcal{L}(\chi, \tau, y) &= \tau - t - y. \end{aligned}$$
The dual function $ q$ is defined as
$$ q(y) = \inf_{x,s}\mathcal{L}(\chi, \tau, y).$$
The optimality conditions for the optimization problem which defines the dual function are $ 0\in \partial_x\mathcal{L}(\chi, \tau, y)$ and $ 0\in\partial_{\tau}\mathcal{L}(\chi, \tau, y)$, therefore, $ q(y)=\mathcal{L}(x^\star(y), t^\star(y), y)$ with
$$ \begin{aligned} &0 \in x^\star - x + y \partial f(x^\star)\\ \Leftrightarrow\ &0 \in (I+y \partial f)(x^\star) - x\\ \Leftrightarrow\ &x \in (I+y \partial f)(x^\star)\\ \Leftrightarrow\ &x^\star(y) = (I+y \partial f)^{-1}(x)\\ \Leftrightarrow\ &x^\star(y) = \mathrm{prox}_{yf}(x), \end{aligned}$$
and
$$\begin{aligned}t^\star(y) = t + y.\end{aligned}$$
Then, the Lagrangian dual function becomes
$$ \begin{aligned} q(y) &= \mathcal{L}(x^\star(y), s^\star(y), y)\\ &= \tfrac{1}{2}\|\mathrm{prox}_{yf}(x)-x\|^2 + y f(\mathrm{prox}_{yf}(x)) + \frac{y^2}{2} - ty\\ &= y f^y(x) + \tfrac{y^2}{2} -(t+y)y\\ &= y (f^y(x) - \tfrac{y}{2} -t), \end{aligned}$$
where $f^y$ is the Moreau envelope function of $f$ with parameter $y$. Then, the dual problem is the following one-dimensional optimization problem
$$ \begin{aligned} \operatorname*{Maximize}_{y\geq 0}\ q(y). \end{aligned}$$
Via proximal operator
Proposition 3 (Projection on epigraph). Let $f:{\rm I\!R}^n\to{\rm I\!R}\cup\{\infty\}$ be a proper, convex, continuous function. For a given $(x, t) \notin \mathrm{epi} f$ and $ \Pi_f(x, t)=(x^{\star},t^{\star})$. Define $h_{t}(x) = \tfrac{1}{2}\max\{0, f(x) - t\}^2$. Then
$$\begin{aligned}x^{\star} {}={}& \mathrm{prox}_{h_{t}}(x), \\ t^{\star} {}={}& f(x^{\star}).\end{aligned}$$
We take the infimum which corresponds to the optimization problem that defines the projection on the epigraph and we have
$$\begin{aligned} &\inf_{\chi, \tau: f(\chi) \leq \tau} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + \tfrac{1}{2}(\tau - t)^2\right\}\\ =&\inf_{\substack{x,\tau,\xi\geq 0 \\ f(\chi) \leq \tau, \tau - t \leq \xi}} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + \tfrac{1}{2}\xi^2\right\}\\ =&\inf_{\chi,\xi\geq 0: f(\chi) \leq t + \xi} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + \tfrac{1}{2}\xi^2\right\}\\ =&\inf_{\chi,\xi\geq 0: f(\chi) - t \leq \xi} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + \tfrac{1}{2}\xi^2\right\}\\ =&\inf_{\chi} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + \underbrace{\tfrac{1}{2}\max\{0, f(\chi) - t\}^2}_{h_t(\chi)}\right\} \\ =&\inf_{\chi} \left\{ \tfrac{1}{2}\|\chi - x\|^2 + h_{t}(\chi)\right\}, \end{aligned}$$
and we notice that this is minimized at $x^{\star} = \mathrm{prox}_{h_{s}}(x),$ and as we know from Proposition 1. $\blacksquare$
Projection on epigraph of exponential function
Let $f(x)=e^x$. Then, from Proposition 1 we have that if $e^x > t$, the projection $(x^\star, t^{\star})$ satisfies
$$x-x^{\star} = (e^{x^{\star}} - t)e^{x^{\star}}.\tag{2}$$
If $t = 0$, the solution of the above equation is
$$x^{\star} = x - \tfrac{1}{2} W_0(2e^{2x}),\tag{3}$$
where $W_0$ is the Lambert $W$ function. In a nutshell,
$$\Pi_{f}(z, 0) = \left(x^{\star}, \exp(x^{\star})\right),$$
where $x^{\star}$ is given by Equation (3), that is,
$$\Pi_{f}(x, 0) = \left(x - \tfrac{1}{2} W_0(2e^{2x}), \exp\left(x - \tfrac{1}{2} W_0(2e^{2x})\right)\right).$$
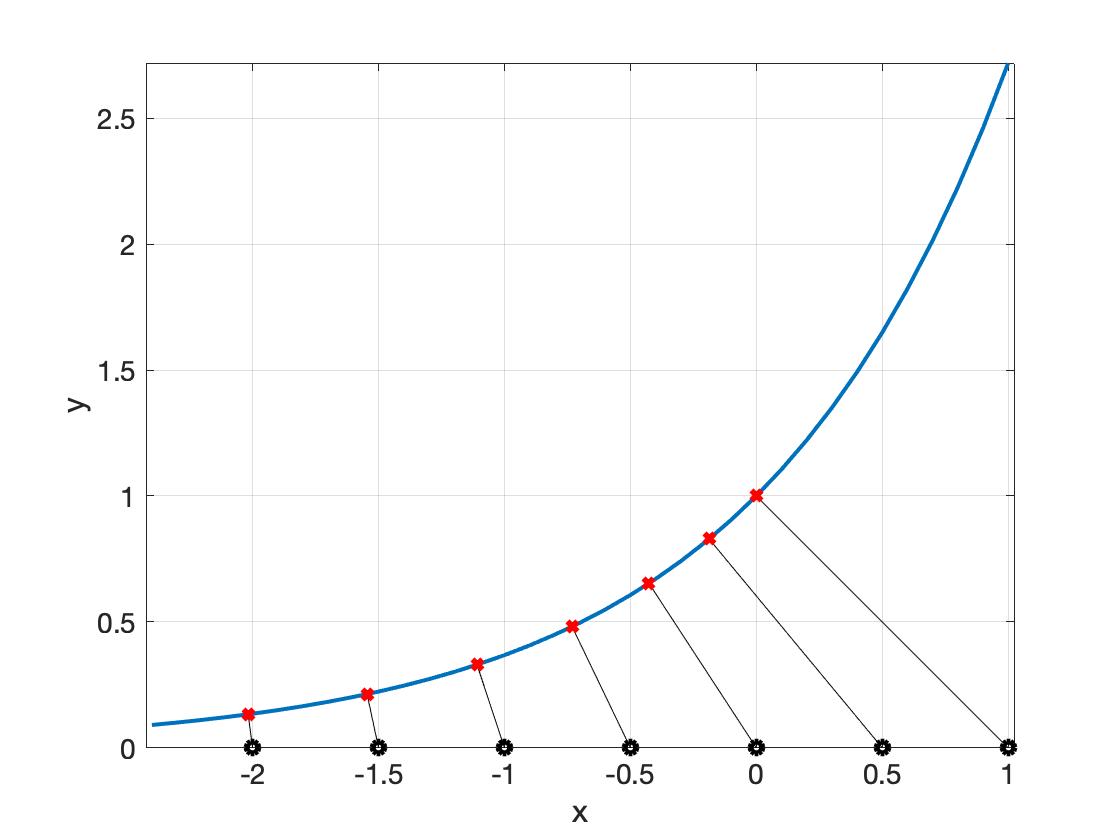
Figure 1. Projection of some points $(x, 0)$ on the epigraph of $f(x) = e^x$.
In the more general case, Equation (2) can be solved numerically.
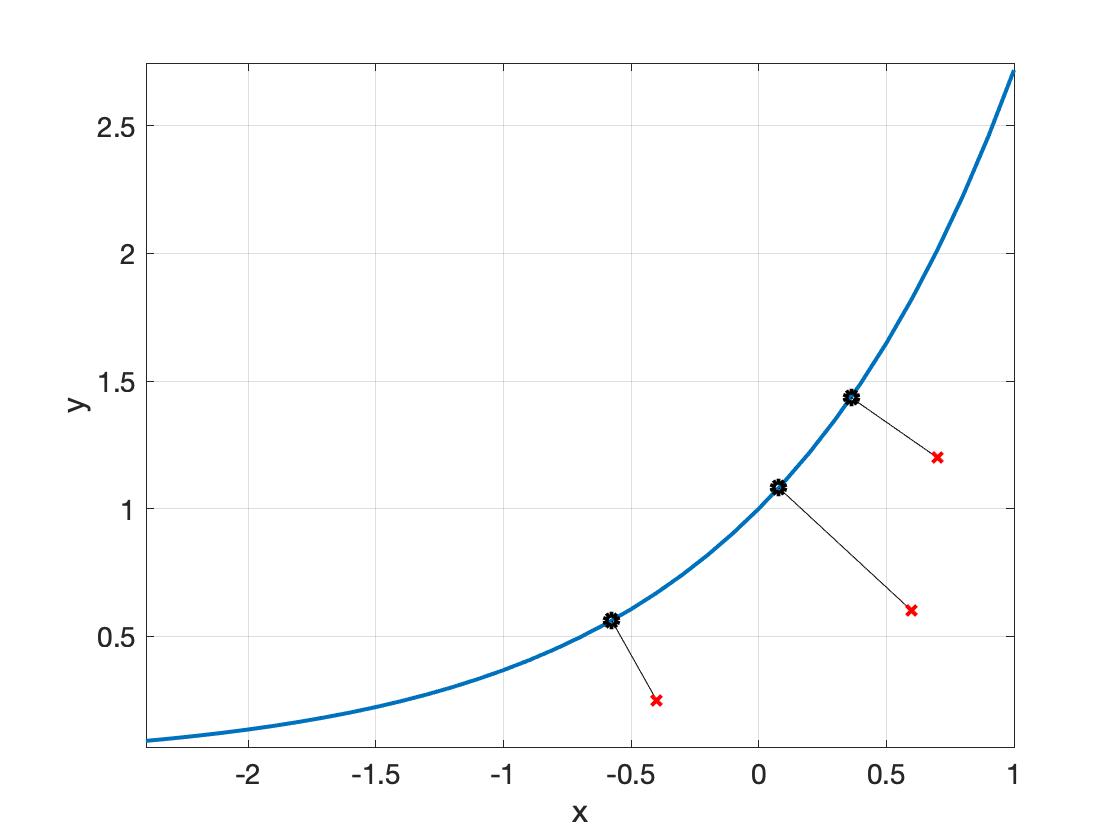
Figure 2. Projection of some points $(x, t)$ on the epigraph of $f(x) = e^x$.