Making sense of tensors and tensor products

I was trying to make sense of tensor products; here are some notes on the topic.

As multilinear maps

Let $(V, +, \cdot)$ be a vector space. Let $r$, $s$ be nonnegative integers. An $(r, s)$-tensor over $V$ - let us call it $T$ - is a multilinear map ^[1], ^[2], ^[3]

$$T:\underbrace{V^* \times \ldots \times V^*}_{r \text{ times}} \times \underbrace{V \times \ldots \times V}_{s \text{ times}} \to {\rm I\!R},$$

where $V^*$ is the dual vector space of $V$ - the space of covectors.

Before we explain what multilinearity is let's give an example.

Let's say $T$ is a $(1, 1)$-tensor. Then $T: V^* \times V \to {\rm I\!R}$, that is $T$ takes a covector and a vector and multilinearity means that for two covectors $\phi, \psi\in V^*$,

$$T(\phi+\psi, v) = T(\phi, v) + T(\psi, v),$$

and

$$T(\lambda \phi, v) = \lambda T(\phi, v),$$

for all $v\in V$, and it is also linear in the second argument, that is,

$$T(\phi, v+w) = T(\phi, v) + T(\phi, w),$$

and

$$T(\phi, \lambda v) = \lambda T(\phi, v).$$

Using these properties twice we can see that

$$T(\phi+\psi, v+w) = T(\phi, v) + T(\phi, w) + T(\psi, v) + T(\psi, w).$$

Example: A $(0, 2)$-tensor. Let us denote the set of polynomials with real coefficients is denoted by $\mathsf{P}$. Define the map

$$g: (p, q) \mapsto g(p, q) \coloneqq \int_0^1 p(x)q(x){\rm d}x.$$

Then this is a $(0, 2)$-tensor,

$$g: \mathsf{P} \times \mathsf{P} \to {\rm I\!R},$$

and multilinearity is easy to check.

It becomes evident that an inner product is a $(0, 2)$-tensor. More precisely, an inner product is a bilinear symmetric positive definite operator $V\times V \to {\rm I\!R}$.

Example: Covectors as tensors. It is easy to see that covectors, $\phi: V\to {\rm I\!R}$ are $(0, 1)$-tensors. Trivially.

Example: Vectors as tensors. Given a vector $v\in V$ we can consider the mapping

$$T_v: V^* \ni \phi \mapsto T_v(\phi) = \phi(v) \in {\rm I\!R}.$$

This makes $T_v$ into a $(1, 0)$-tensor.

Example: linear maps as tensors. We can see a linear map $\phi \in {\rm Hom}(V, V)$ as a $(1,1)$-tensor

$$T_\phi: V^* \times V \ni (\psi, v) \mapsto T_\phi(\psi, v) = \psi(\phi(v)) \in {\rm I\!R}.$$

Components of a tensor

Let $T$ be an $(r, s)$-tensor over a finite-dimensional vector space $V$ and let $\{e_i\}_i$ be a basis for $V$. Let the dual basis, for $V^*$, be $\{\epsilon^i\}_i$. The two bases have the same cardinality. Then define the $(r+s)^{\dim V}$ many numbers

$$T^{i_1, \ldots, i_r}_{j_1, \ldots, j_s} = T(\epsilon^{i_1}, \ldots, \epsilon^{i_r}, e_{j_1}, \ldots, e_{j_s}).$$

These are the components of $T$ with respect to the given basis.

This allows us to conceptualise a tensor as a multidimensional (multi-indexed) array. But maybe we shouldn’t… This is as bad as treating vectors as sequences of numbers, or matrices as “tables” instead of elements of a vector space and linear maps respectively.

Let's see how exactly this works via an example ^[4]. Indeed, consider an $(2,3)$-tensor of the tensor space $\mathcal{T}^{2}_{3} = V^{\otimes 2} \otimes (V^*)^{\otimes 3}$ , which can be seen as a multilinear map

$$T:V^*\times V^*\times V \times V \times V \to {\rm I\!R}.$$

Yes, we have two $V^*$ and three $V$!

Take a basis $(e_i)_i$ of $V$ and a basis $(\theta^j)_j$ of $V^*$. Let us start with an example using a pure tensor of the form $e_{i_1}\otimes e_{i_2} \otimes e_{i_3} \otimes \theta^{j_1} \otimes \theta^{j_2},$ for some indices $i_1,i_2,i_3$ ,and $j_1, j_2$. This can be seen as a map $V^*\times V^*\times V \times V \times V \to {\rm I\!R}$, which is defined as

$$\begin{aligned}(\theta^{j_1} \otimes \theta^{j_2} \otimes e_{i_1}\otimes e_{i_2} \otimes e_{i_3}) (\bar{e}_1, \bar{e}_2, \bar{\theta}^1, \bar{\theta}^2, \bar{\theta}^3) \\ {}={} \langle \theta^{j_1}, \bar{e}_1\rangle \langle \theta^{j_2}, \bar{e}_2\rangle \langle e_{i_1}, \bar{\theta}^1\rangle \langle e_{i_2}, \bar{\theta}^2\rangle \langle e_{i_3}, \bar{\theta}^3\rangle,\end{aligned}$$

where $\langle {}\cdot{}, {}\cdot{}\rangle$ is the natural pairing between $V$ and its dual, so

$$\begin{aligned} (\theta^{j_1} \otimes \theta^{j_2} \otimes e_{i_1}\otimes e_{i_2} \otimes e_{i_3}) (\bar{e}_1, \bar{e}_2, \bar{\theta}^1, \bar{\theta}^2, \bar{\theta}^3) \\{}={} \theta^{j_1}(\bar{e}_1) \theta^{j_2}(\bar{e}_2) \bar{\theta}^1(e_{i_1}) \bar{\theta}^2(e_{i_2}) \bar{\theta}^3(e_{i_3}).\end{aligned}$$

More specifically, when the above tensor is applied to a basis vector $(e_{i_1'}, e_{i_2'}, \theta^{j_1'}, \theta^{j_2'}, \theta^{j_3'})$, then the result is

$$\begin{aligned} &(\theta^{j_1} \otimes \theta^{j_2} \otimes e_{i_1}\otimes e_{i_2} \otimes e_{i_3}) (e_{i_1'}, e_{i_2'}, \theta^{j_1'}, \theta^{j_2'}, \theta^{j_3'}) \\ {}={}& \theta^{j_1}(e_{i_1'}) \theta^{j_2}(e_{i_2'}) \theta^{j_1'}(e_{i_1}) \theta^{j_2'}(e_{i_2}) \theta^{j_3'}(e_{i_3}) \\ {}={}& \delta_{i_1' j_1} \delta_{i_2' j_2} \delta_{i_1 j_1'} \delta_{i_2 j_2'} \delta_{i_3 j_3'}. \end{aligned}$$

A general tensor of $\mathcal{T}^{2}_{3}$ has the form

$$T {}={} \sum_{ \substack{i_1, i_2, i_3 \\ j_1, j_2} } T_{j_1, j_2}^{i_1, i_2, i_3} (\theta^{j_1} \otimes \theta^{j_2} \otimes e_{i_1}\otimes e_{i_2} \otimes e_{i_3}),$$

for some parameters (components) $T_{j_1, j_2}^{i_1, i_2, i_3}$. This can be seen as a mapping $T:V^*\times V^* \times V^* \times V \times V \to {\rm I\!R}$ that acts on elements of the form

$$x {}={} \left( \sum_{j_1}a^1_{j_1}\theta^{j_1}, \sum_{j_2}a^2_{j_2}\theta^{j_2}, \sum_{j_3}a^3_{j_3}\theta^{j_3}, \sum_{i_1}b^1_{i_1}e_{i_1}, \sum_{i_2}b^1_{i_2}e_{i_2}, \sum_{i_3}b^1_{i_3}e_{i_3} \right),$$

and gives

$$\begin{aligned} Tx {}={}& \sum_{ \substack{i_1, i_2, i_3 \\ j_1, j_2} } T_{j_1, j_2}^{i_1, i_2, i_3} (e_{i_1}, e_{i_2}, e_{i_3}, \theta^{j_1}, \theta^{j_2})(x) \\ {}={}& \sum_{ \substack{i_1, i_2, i_3 \\ j_1, j_2} } T_{j_1, j_2}^{i_1, i_2, i_3} \left\langle e_{i_1}, \sum_{j_1'}a^1_{j_1'}\theta^{j_1'}\right\rangle \left\langle e_{i_2}, \sum_{j_2'}a^1_{j_2'}\theta^{j_2'}\right\rangle \\ &\qquad\qquad\qquad\left\langle e_{i_3}, \sum_{j_3'}a^1_{j_3'}\theta^{j_3'}\right\rangle \left\langle \theta_{j_1}, \sum_{i_1'}b^1_{i_1'}e^{i_1'}\right\rangle \left\langle \theta_{j_2}, \sum_{i_2'}b^2_{i_2'}e^{i_2'}\right\rangle \\ {}={}& \sum_{ \substack{i_1, i_2, i_3 \\ j_1, j_2} } T_{j_1, j_2}^{i_1, i_2, i_3} a^1_{i_1}a^2_{i_2}a^3_{i_3}b^1_{j_1}b^1_{j_2}. \end{aligned}$$

As a quotient on a huge space

Here we construct a huge vector space and apply a quotient to enforce the axioms we expect tensors and tensor products to have. This huge space is a space of functions sometimes referred to as the "formal product" ^[5]. See also this video ^[7].

We will define the tensor product of two vector spaces. Let $V, W$ be two vector spaces. We define a vector space $V*W$, which we will call the formal product of $V$ and $W$, as the linear space that has $V\times W$ as a Hamel basis. This space is also known as the free vector space, $V*W = {\rm Free}(V\times W)$.

To make this more concrete, we can identify $V*W$ by the space of functions $\varphi: V\times W \to {\rm I\!R}$ with finite support. Representatives (and a basis) for this set are the functions

$$\delta_{v, w}(x, y) {}={} \begin{cases} 1, & \text{ if } (x,y)=(v,w) \\ 0,& \text{ otherwise} \end{cases}$$

Indeed, every function $f:V\times W\to{\rm I\!R}$ with finite support (a function of $V*W$) can be written as a finite combination of such $\delta$ functions and each $\delta$ function is identified by a pair $(v,w)\in V\times W$.

Note that $V\times W$ is a vector space when equipped with the natural operations of function addition and scalar multiplication.

We consider the natural embedding, $\delta$, of $V\times W$ into $V*W$, which is naturally defined as

$$\delta:V\times W \ni (v_0, w_0) \mapsto \delta_{v_0, w_0} \in V * W.$$

Consider now the following subspace of $V*W$

$$M_0 {}={} \operatorname{span} \left\{ \begin{array}{l} \delta(v_1+v_2, w) - \delta(v_1, w) - \delta(v_2, w), \\ \delta(v, w_1+w_2) - \delta(v, w_1) - \delta(v, w_2), \\ \delta(\lambda v, w) - \lambda \delta(v, w), \\ \delta(v, \lambda w) - \lambda \delta(v, w), \\ v, v_1, v_2 \in V, w, w_1, w_2 \in W, \lambda \in {\rm I\!R} \end{array} \right\}$$

Quotient space definition of tensor space.

We define the tensor product of $V$ with $W$ as $$V\otimes W = \frac{V * W }{M_0}.$$ This is called the tensor space of $V$ with $W$ and its elements are called tensors.

This is the space we were looking for. Here's what we mean: we have already defined the mapping $\delta: V\times W \to V * W$. We also define the canonical embedding $\pi: V*W \to V \otimes M_0$. We then define the tensor product of $v\in V$ and $w\in W$ as

$$v\otimes w = (\pi {}\circ{} \delta)(v, w) = \delta_{v, w} {}+{} M_0.$$

It is a mapping $\otimes: V\times W \to V\otimes W$ and we can see that it is bilinear.

Properties of $\otimes$.

The operator $\otimes$ is bilinear.

Proof. For $v\in V$, $w\in W$ and $\lambda \in {\rm I\!R}$ we have

$$\begin{aligned} (\lambda v)\otimes w {}={}& \delta_{\lambda v, w} + M_0 \\ {}={}& \underbrace{\delta_{\lambda v, w} - \lambda \delta_{v, w}}_{\in{}M_0} + \lambda \delta_{v, w} + M_0 \\ {}={}& \lambda \delta_{v, w} + M_0 \\ {}={}& \lambda (\delta_{v, w} + M_0) \\ {}={}& \lambda (v\otimes w). \end{aligned}$$

Likewise, for $v_1, v_2 \in V$, $w\in W$, $\lambda \in {\rm I\!R}$,

$$\begin{aligned} (v_1 + v_2)\otimes w {}={}& \delta_{v_1+v_2, w} + M_0 \\ {}={}& \underbrace{\delta_{v_1+v_2, w} - \delta_{v_1, w} -\delta_{v_2, w}}_{\in {} M_0} + \delta_{v_1, w} + \delta_{v_2, w} + M_0 \\ {}={}& \delta_{v_1, w} + \delta_{v_2, w} + M_0 \\ {}={}& (\delta_{v_1, w} + M_0) + (\delta_{v_2, w} + M_0) \\ {}={}& v_1\otimes w + v_2 \otimes w \end{aligned}$$

The other properties are proved likewise. $\Box$

Universal property

Here's how I understand the universal property: Suppose we know that we have a function $f: V\times W \to{} ?$, which is bilinear. We can always think of the mysterious space $?$ as the tensor space $V\otimes W$ ^[5].

Let's look at Figure 1.

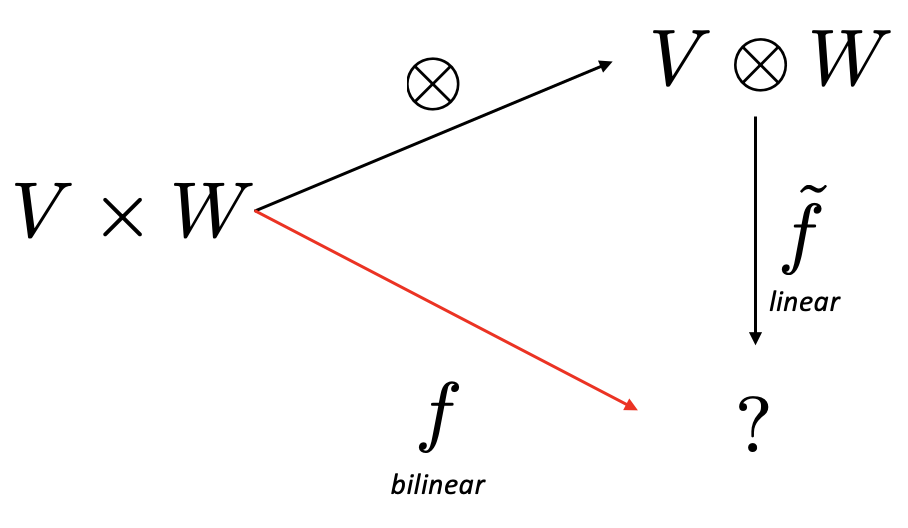
Figure 1. Universal property of tensor product.

There is a unique linear function $\tilde{f}:V\otimes W \to{} ?$ such that

$$f(v, w) = \tilde{f}(v\otimes w).$$

Let us underline that $\tilde{f}$ is linear! This makes $\otimes$ a prototype bilinear function as any other bilinear function is a linear map of precisely this one.

Dimension

Let $V$ and $W$ be finite dimensional. We will show that

Dimension of tensor

$$\dim(V\otimes W) = \dim V \dim W.$$

Proof 1. To that end we use the fact that the dual vector space has the same dimension as the original vector space. That is, the dimension of $V\otimes W$ is the dimension of $(V\otimes W)^*.$

The space $(V\otimes W)^* = {\rm Hom}(V\otimes W, {\rm I\!R})$ is the space of bilinear maps $V\times W \to {\rm I\!R}$.

Suppose $V$ has the basis $\{e^V_1, \ldots, e^V_{n_V}\}$ and $W$ has the basis $\{e^W_1, \ldots, e^W_{n_W}\}$.

To form a basis for the space of bilinear maps $f:V\times W\to{\rm I\!R}$ we need to identify every such function with a sequence of scalars. We have

$$f(u, v) = f\left(\sum_{i=1}^{n_V}a^V_{i}e^V_{i}, \sum_{i=1}^{n_W}a^W_{i}e^W_{i}\right).$$

From the bilinearity of $f$ we have

$$f(u, v) = \sum_{i=1}^{n_V}\sum_{j=1}^{n_W} a^V_{i}a^W_{j} f(e^V_{i}, e^{W}_{j}).$$

The right hand side is a bilinear function and the coefficients $(a^V_i, a^W_j)$ suggest that the dimension if $n_V n_W$. $\Box$

Proof. This is due to ^[22]. We can write any $T \in V\otimes W$ as

$$T = \sum_{k=1}^{n}a_k \otimes b_k,$$

for $a_k\in V$ and $b_k\in W$ and some finite $n$. If we take bases $\{v_i\}_{i=1}^{n_V}$ and $\{w_i\}_{i=1}^{n_W}$ we can write

$$a_k = \sum_{i=1}^{n_V}\alpha_{ki}v_i,$$

and

$$b_k = \sum_{j=1}^{n_W}\beta_{kj}w_j,$$

therefore,

$$\begin{aligned}T {}={}& \sum_{i=1}^{n}\left(\sum_{i=1}^{n_V}\alpha_{ki}v_i\right) \otimes\left(\sum_{j=1}^{n_W}\beta_{kj}w_j\right) \\ {}={}& \sum_{i=1}^{n} \sum_{i=1}^{n_V} \sum_{j=1}^{n_W} \alpha_{ki}\beta_{kj} v_i\otimes w_j. \end{aligned}$$

This means that $\{v_i\otimes w_j\}$ is a basis of $V\otimes W$.

Tensor basis

In the finite-dimensional case, the basis of $V\otimes W$ can be constructed from the bases of $V$ and $W$, $\{e^V_1, \ldots, e^V_{n_V}\}$ and $\{e^W_1, \ldots, e^W_{n_W}\}$ as the set

$$\mathcal{B}_{V\otimes W} = \{e^V_i \otimes e^{W}_j, i=1,\ldots, n_V, j=1,\ldots, n_W\}.$$

This implies that

$$\dim (V\otimes W) = \dim V \dim W.$$

Tensor products of spaces of functions

We need first to define the function space $F(S)$ as in Kostrikin^[2].

Let $S$ be any set. We define the set $F(S)$—we can denote it also as ${\rm Funct}(S, {\rm I\!R})$—as the set of all functions from $S$ to ${\rm I\!R}$. If $f\in F(S)$, then $f$ is a function $f:S\to{\rm I\!R}$ and $f(s)$ denotes the value at $s\in S$.

On $F(S)$ we define addition and scalar multiplication in a pointwise manner: For $f, g\in F(S)$ and $c\in {\rm I\!R}$,

$$\begin{aligned} (f+g)(s) {}={}& f(s) + g(s), \\ (cf)(s) {}={}& c f(s). \end{aligned}$$

This makes $F(S)$ into a vector space. Note that $S$ is not necessarily a vector space.

If $S = \{s_1, \ldots, s_n\}$ is a finite set, $F(S)$ can be identified with ${\rm I\!R}^n$. After all, for every $f\in F(S)$ all you need to know is $f(s_1), \ldots, f(s_n)$.

Every element $s\in S$ is associated with the delta function

$$\delta_{s}(\sigma) = \begin{cases} 1, &\text{ if } \sigma = s, \\ 0, &\text{ otherwise} \end{cases}$$

The function $\delta_s:S \to \{0,1\}$ is called Kronecker's delta.

If $S$ is finite, then every $f\in S$ can be written as

$$f = \sum_{s\in S} a_s \delta_s.$$

Let $S_1$ and $S_2$ be finite sets and let $F(S_1)$ and $F(S_2)$ be the corresponding function spaces. Then, there is a canonical identity of the form

$$\underbrace{F(\underbrace{S_1 \times S_2}_{\text{Finite set of pairs}})}_{\text{Has }\delta_{s_1, s_2}\text{ as basis}} = F(S_1) \otimes F(S_2),$$

which associates each function $\delta_{s_1, s_2}$ with $\delta_{s_1} \otimes \delta_{s_2}$.

If $f_1 \in F(S_1)$ and $f_2 \in F(S_2)$ then using the standard bases of $F(S_1)$ and $F(S_2)$

$$f_1 \otimes f_2 = \left(\sum_{s_1 \in S_1}f_1(s_1) \delta_{s_1}\right) \otimes \left(\sum_{s_1 \in S_2}f_2(s_2) \delta_{s_2}\right).$$

Isomorphism $(U\otimes V)^* \cong U^* \otimes V^*$.

We have the isomorphism of vector spaces $(U\otimes V)^* \cong U^* \otimes V^*$ with isomorphism map

$$\rho:U^* \otimes V^* \to (U\otimes V)^*,$$

where for $f\in U^*$ and $g\in V^*$,

$$\rho(f\otimes g)(u\otimes v) = f(u)g(v).$$

For short, we write $(f\otimes g)(u\otimes v) = f(u)g(v)$.

Roman ^[5] in Theorem 14.7 proves that $\rho$ is indeed an isomorphism.

Associativity

As Kostrikin notes ^[2], the spaces $(L_1\otimes L_2)\otimes L_3$ and $L_1 \otimes (L_2 \otimes L_3)$ do not coincide — they are spaces of different type. They, however, can be found to be isomorphic via a canonical isomorphism.

We will start by studying the relationship between $L_1 \otimes L_2 \otimes L_3$ and $(L_1 \otimes L_2) \otimes L_3$.

The mapping $L_1 \times L_2 \ni (l_1, l_2) \mapsto l_1 \otimes l_2 \in L_1 \otimes L_2$ is bilinear, so the mapping

$$L_1 \times L_2 \times L_2 \ni (l_1, l_2, l_3) \mapsto (l_1 \otimes l_2) \otimes l_2 \in (L_1 \otimes L_2) \otimes L_3$$

is trilinear, so it can be constructed via the unique linear map

$$L_1 \otimes L_2 \otimes L_3 \to (L_1 \otimes L_2) \otimes L_3,$$

that maps $l_1 \otimes l_2 \otimes l_3$ to $(l_1 \otimes l_2) \otimes l_3$. Using bases we can show that this map is an isomorphism.

Commutativity and the braiding map

See Wikipedia.

As a note, take $x = (x_1, x_2)$ and $y = (y_1, y_2)$. Then $x\otimes y$ and $y\otimes x$ look like

$$\begin{bmatrix}x_1y_1\\x_1y_2\\x_2y_1\\x_2y_2\end{bmatrix}, \begin{bmatrix}x_1y_1\\x_2y_1\\x_1y_2\\x_2y_2\end{bmatrix}$$

and we see that the two vectors contain the same elements in different order. In that sense,

$$V\otimes W \cong W \otimes V.$$

The corresponding map, $V\otimes V \ni v\otimes v' \mapsto v'\otimes v \in V\otimes V$ is called the braiding map and it induces an automorphism on $V\otimes V$.

Some key isomorphisms

Result 1: Linear maps as tensors

This is only true in the finite dimensional case.

To prove this we build a natural isomorphism

$$\Phi:V^*\otimes W \to {\rm Hom}(V, W),$$

by defining

$$\Phi(v^*\otimes w)(v) = v^*(v)w.$$

Note that $v^*\otimes w$ is a pure tensor. A general tensor has the form

$$\sum_i v_i^*\otimes w_i,$$

and

$$\Phi\left(\sum_i v_i^*\otimes w_i\right)(v) = \sum_i v_i^*(v)w_i.$$

This is a linear map. Linearity is easy to see. See also this video ^[6].

Here is the statement:

First isomorphism result: ${\rm Hom}(V, W) \cong V^* \otimes W$.

In the finite-dimensional case, we have that ${\rm Hom}(V, W) \cong V^* \otimes W$ holds with isomorphism $\phi \otimes w \mapsto (v \mapsto \phi(v)w).$

Proof. ^[10] The proposed map, $\phi \otimes w \mapsto (v \mapsto \phi(v)w)$, is a linear map $V^*\otimes W\to {\rm Hom}(V, W)$. We will construct its inverse (and prove that it is the inverse). Let $(e_i)_i$ be a basis for $V$. Let $(e_i^*)_i$ be the naturally induced basis of the dual vector space, $V^*$. We define the mapping

$$g:{\rm Hom}(V, W) \ni \phi \mapsto \sum_{i}e_i^* \otimes \phi(e_i) \in V^*\otimes W.$$

We claim that $g$ is the inverse of $\Phi$ which we already defined to be the map $V^*\otimes W \to {\rm Hom}(V, W)$ given by $\Phi(v^*\otimes w)(v) = v^*(v)w.$ Indeed, we see that

$$\begin{aligned} \Phi(g(\phi)) {}={}& \Phi\left(\sum_{i=1}^{n}e_i^* \otimes \phi(e_i)\right) &&\text{Definition of $g$} \\ {}={}& \sum_{i=1}^{n} \Phi\left(e_i^* \otimes \phi(e_i)\right) &&\text{$\Phi$ is linear} \\ {}={}& \sum_{i=1}^{n}e_i^*({}\cdot{})\phi(e_i) \\ {}={}& \phi\left(\underbrace{e_i^*({}\cdot{})e_i}_{{\rm id}}\right) && \text{$\phi$ is linear} \\ {}={}& \phi. \end{aligned}$$

Conversely,

$$\begin{aligned} g(\Phi(v^*\otimes w)) {}={}& g(v^*(\cdot)w) \\ {}={}& \sum_{i=1}^{n}e_i^* \otimes v^*(e_i)w \\ {}={}& \left(\sum_{i=1}^{n}e_i^* v^*(e_i)\right) \otimes w \\ {}={}& v^*\otimes w. \end{aligned}$$

This completes the proof. $\Box$

Result 2: Dual of space of linear maps

For two finite-dimensional spaces $V$ and $W$, it is

$$\begin{aligned} {\rm Hom}(V, W)^* {}\cong{} (V^*\otimes W)^* {}\cong{} V^{**}\otimes W^* {}\cong{} V\otimes W^* {}\cong{} {\rm Hom}(W, V). \end{aligned}$$

It is ${\rm Hom}(V, W)^* {}\cong{} {\rm Hom}(W, V).$

Some additional consequences of this are:

${\rm Hom}({\rm Hom}(V,W),U) \cong {\rm Hom}(V,W)^*\otimes U \cong (V^*\otimes W)^*\otimes U \cong V\otimes W^* \otimes U.$
$U\otimes V \otimes W \cong {\rm Hom}(U^*, V)\otimes W \cong {\rm Hom}({\rm Hom}(V,U^*),W)$
$V\otimes V^* \cong {\rm Hom}(V^*, V) \cong {\rm Hom}(V,V)$, where if $V$ is finite dimensional, $V^*\cong V$, so we see that $V^*\otimes V \cong {\rm End}(V)$

Question: How can we describe linear maps from ${\rm I\!R}^{m\times n}$ to ${\rm I\!R}^{p\times q}$ with sensors?

We are talking about the space ${\rm Hom}({\rm I\!R}^{m\times n}, {\rm I\!R}^{p\times q})$, but every matrix $A$ can be identified by the linear map $x\mapsto Ax$, so ${\rm I\!R}^{m\times n}\cong {\rm Hom}({\rm I\!R}^{n}, {\rm I\!R}^{m})$, so

$$\begin{aligned} {\rm Hom}({\rm I\!R}^{m\times n}, {\rm I\!R}^{p\times q}) {}\cong{}& {\rm Hom}({\rm Hom}({\rm I\!R}^n, {\rm I\!R}^m), {\rm Hom}({\rm I\!R}^q, {\rm I\!R}^p)) \\ {}\cong{}& (({\rm I\!R}^n)^*\otimes {\rm I\!R}^m)^* \otimes ({\rm I\!R}^{q})^*\otimes {\rm I\!R}^p \\ {}\cong{}& {\rm I\!R}^n \otimes {\rm I\!R}^{m*} \otimes {\rm I\!R}^{q*} \otimes {\rm I\!R}^p \end{aligned}$$

Such objects can be seen as multilinear maps ${\rm I\!R}^{n*} \times {\rm I\!R}^{m} \times {\rm I\!R}^{q} \times {\rm I\!R}^{p*} \to {\rm I\!R}$ , that is,

$$(x\otimes \phi \otimes \psi \otimes y)(\theta, s, t, \zeta) = \theta(x)\phi(s)\psi(t)\zeta(y).$$

Lastly,

$$\dim {\rm Hom}({\rm I\!R}^{m\times n}, {\rm I\!R}^{p\times q}) = \dim {\rm I\!R}^n \otimes {\rm I\!R}^{m*} \otimes {\rm I\!R}^{q*} \otimes {\rm I\!R}^p = nmpq.$$

Result 3: Tensor product of linear maps

Tensor product of linear maps. Let $U_1, U_2$ and $V_1, V_2$ be vector spaces. Then

$${\rm Hom}(U_1, U_2) \otimes {\rm Hom}(V_1, V_2) \cong {\rm Hom}(U_1\otimes V_1, U_2\otimes V_2)$$

with isomorphism function

$$(\phi\otimes\psi)(u\otimes v) = \phi(u) \otimes \psi(v).$$

Again, using the universal property

We can define $V\otimes W$ to be the a space accompanied by a bilinear operation $\otimes: V\times W \to V \otimes W$ that has the universal property in the following sense: ^[5]

Universal property. If $f: V\times W \to Z$ is a bilinear function, then there is a unique linear function $\tilde{f}: V\otimes Z$ such that $f = \tilde{f} \circ \otimes$.

The universal property says that every bilinear map $f(u, v)$ on a vector space $V$ is a linear function $\tilde{f}$ of the tensor product, $\tilde{f}(u\otimes v)$ ^[6].

See more about the uniqueness of tensor product via the universality-based definition as well as^[8].

Making sense of tensors using polynomials

This is based on^[9]. We can identify vectors $u=(u_0, \ldots, u_{n-1})\in{\rm I\!R}^n$ and $v\in{\rm I\!R}^m$ as polynomials over ${\rm I\!R}$ of the form

$$u(x) = u_0 + u_1x + \ldots + u_{n-1}x^{n-1}.$$

We know that a pair of vectors lives in the Cartesian product space ${\rm I\!R}^n\times {\rm I\!R}^m$. A pair of polynomials lives in a space with basis

$$\mathcal{B}_{\rm prod} {}\coloneqq{} \{(1, 0), (x, 0), \ldots, (x^{n-1}, 0)\} \cup \{(0, 1), (0, y), \ldots, (0, y^{n-1})\}.$$

But take now two polynomials $u$ and $v$ and multiply them to get

$$u(x)v(y) = \sum_{i}\sum_{j}c_{ij}x^iy^j.$$

The result is a polynomial of two variables, $x$ and $y$. This corresponds to the tensor product of $u$ and $v$.

References

F. Schuller, Video lecture 3, Accessed on 12 Sept 2023.
А. И. Кострикин, Ю.И.Манин, Линейная алгебра и геометрия , Часть 4

Wikipedia, tensor product on Wikipedia, Accessed on 15 Sept 2023.
P. Renteln, Manifolds, Tensors, and Forms: An introduction for mathematicians and physicists, Cambridge University Press, 2014.
Steven Roman, Advanced Linear Algebra, Springer, 3rd Edition, 2010
Check out this guy on YouTube (@mlbaker) gives a cool construction and explanation of tensors
M. Penn's video "What is a tensor anyway?? (from a mathematician)" on YouTube
Proof: Uniqueness of the Tensor Product, YouTube video by Mu Prime Math
Prof Macauley on YouTube, Advanced Linear Algebra, Lecture 3.7: Tensors, accessed on 9 November 2023; see also his slides, Lecture 3.7: Tensors, lecture slides on tensors, some nice diagrams and insights.
Answer on MSE on why ${\rm Hom}(V, W)$ is the same thing as $V^*\otimes W$, accessed on 9 November 2023
Lots of books on tensors, tensor calculus, and applications to physics can be found on this GitHub repo, accessed on 9 November 2023
S. Treil, Linear algebra done wrong, Chapter 8: dual spaces and tensors, 2017
A. Defant and K. Floret, Tensor norms and operator ideals (link), North Holand, 1993
K. Purbhoo, Notes on Tensor Products and the Exterior Algebra for Math 245, link
Lecture notes on tensors, Uni Berkeley, link
J. Zintl, Notes on tensor products, part 3, link
Rich Schwartz, Notes on tensor products
J. Zintl, Notes on multilinear maps, link
A Iozzi, Multilinear Algebra and Applications. Concise (100 pages), very clear explanation.
MIT Multilinear algebra lecture notes/book, multilinear algebra, introduction (dual spaces, quotients), tensors, the pullback operation, alternating tensors, the space $\Lambda^k(V^*)$, the wedge product, the interior product, orientations, and more 👍 (must read)
JR Ruiz-Tolosa and E Castillo, From vectors to tensors, Springer, Universitext, 2005.
Elias Erdtman, Carl Jonsson, Tensor Rank, Applied Mathematics, Linkopings Universite, 2012

As multilinear maps#

Components of a tensor#

As a quotient on a huge space#

Universal property#

Dimension#

Tensor basis#

Tensor products of spaces of functions#

Associativity#

Commutativity and the braiding map#

Some key isomorphisms#

Result 1: Linear maps as tensors#

Result 2: Dual of space of linear maps#

Result 3: Tensor product of linear maps#

Again, using the universal property#

Making sense of tensors using polynomials#

Further reading#

References#