Tensor product via universality

We start by defining the tensor product of two vector spaces $V$ and $W$ via the universal property. Recall the definition of the tensor product of two vector spaces using the approach of universality^{[1] [2] [3]}

Definition: tensor product. Let $V$ and $W$ be two vector spaces. The tensor product of $V$ and $W$ is a vector space $T$ along with a bilinear map $\tau:V\times W \to T$ such that for every bilinear map

$$f:V\times W \to U,$$

where $U$ is a vector space, there is a unique linear map $\tilde{f}:T\to U$ such that

$$\tilde{f} \circ \tau = f,$$

i.e., the following diagram commutes

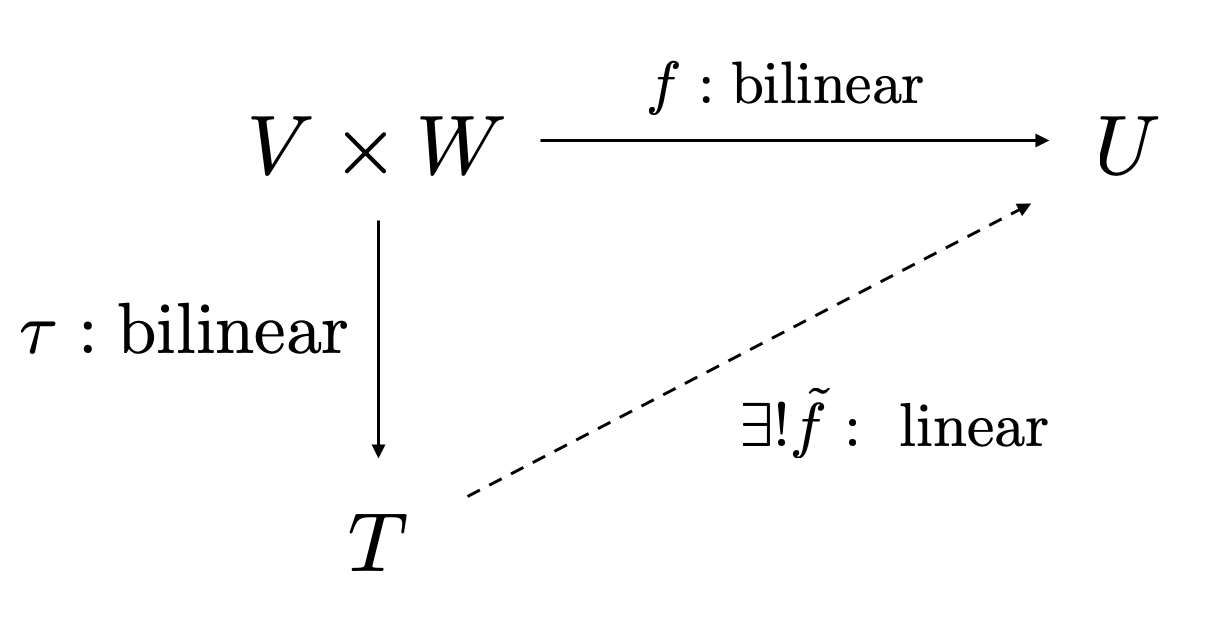
Figure 1. Commutative diagram demonstrating the universal property.

The mysterious vector space $T$ is called the tensor product of $V$ and $W$ and can be denoted by $T = V\otimes W$. The bilinear map $\tau$ is called the tensor product bilinear map, or just tensor product of two vectors; we also denote $\tau(u, v) = u \otimes v$.

Note that a tensor product is a pair of a vector space, $V\otimes W$ and a bilinear map, $\tau: V\times W \to V\otimes W$.

We prove the following^[2]

Proof. We apply the definition of the tensor product with $\tau_2$ in place of the bilinear map $f$ and using the tensor product space $T_1$ as in the following graph

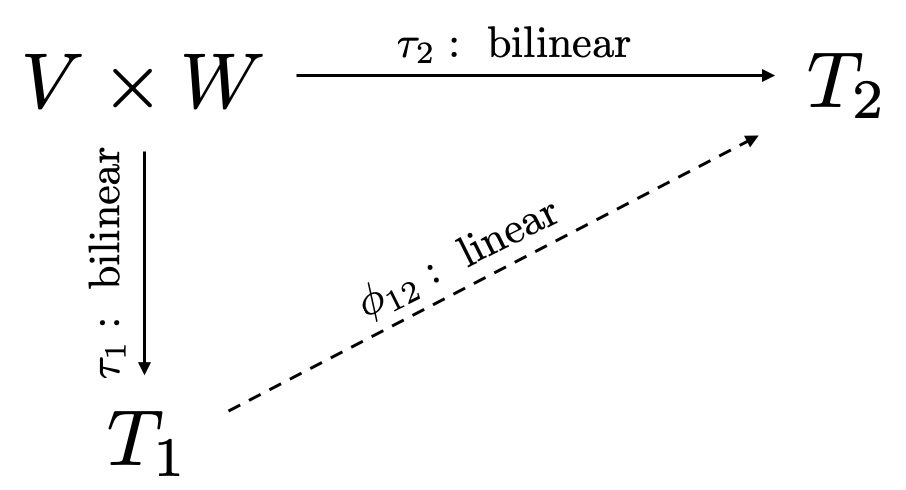
Figure 2. Commutative diagram.

From Figure 2 we see that

$$\tau_2 = \phi_{12} \circ \tau_1.\tag{1}$$

Next, we swap $T_1$ and $T_2$...

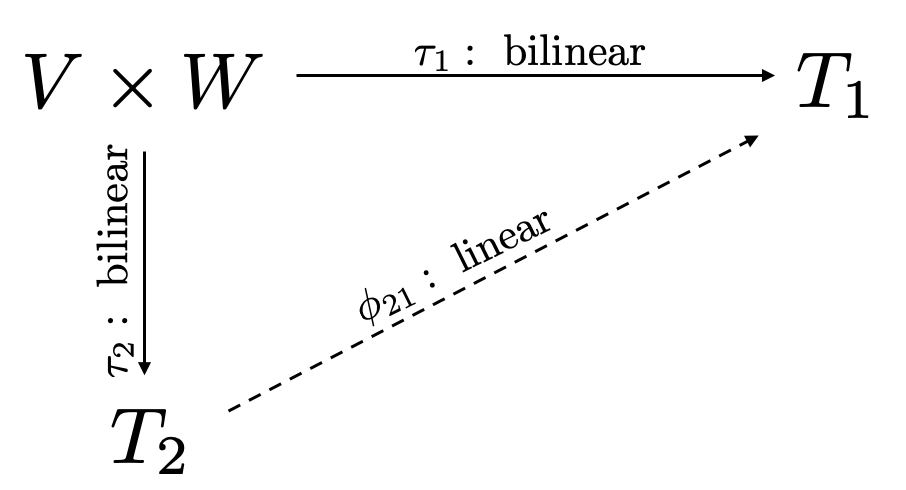
Figure 3. Commutative diagram.

We see that

$$\tau_1 = \phi_{21}\circ \tau_2.\tag{2}$$

From Equations (1) and (2),

$$\tau_1 = \phi_{21}\circ \phi_{12}\circ \tau_1.\tag{3}$$

This makes us suspect that $\phi_{12} = \phi_{21}^{-1}$. To prove this, we put $T_1$ in both places in the commutative diagram as follows:

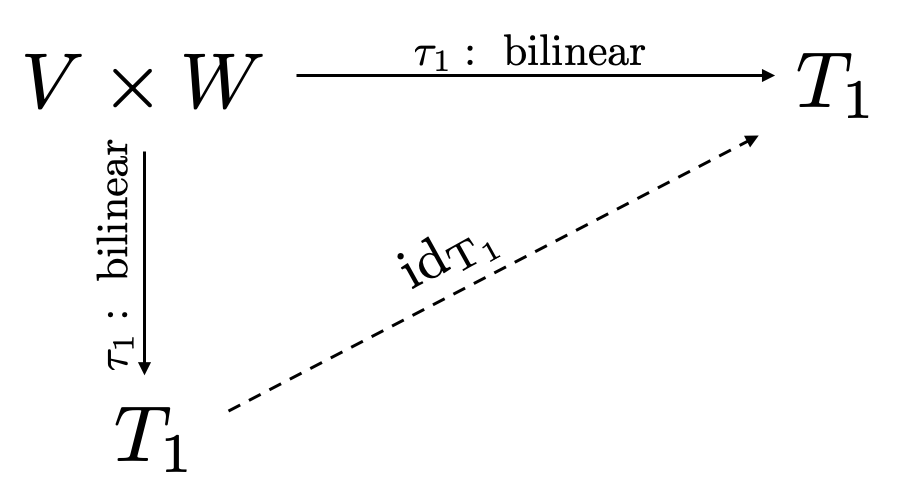
Figure 4. Commutative diagram with $T_1$ and $T_1$ (twice).

By the uniqueness of the linear map $T_1\to T_1$ and since ${\rm id}_{T_1}:T_1\to T_1$ does the job we conclude that only ${\rm id}_{T_1}$ is such that ${\rm id}_{T_1} \circ \tau_1 = \tau_1$, so in Equation (3) we have

$$\phi_{12}\circ \phi_{21} = {\rm id}_{T_1}.\tag{4}$$

Likewise, we can show that

$$\phi_{21}\circ \phi_{12} = {\rm id}_{T_{2}}.\tag{5}$$

The map $\phi_{12}:T_1 \to T_2$ is a vector space isomorphism, which completes the proof. $\Box$

Existence

The existence of the tensor product is established constructively using the concept of the free vector space. The above definition of course does not prove that the tensor product exists, and neither does the uniqueness statement above.

Example: trace

The mapping $\langle {}\cdot{}, {}\cdot{}\rangle: V^*\times V\to \R$ defined as $\langle f, v\rangle = f(v)$ is the natural pairing of $V$ and its dual map. It is easy to see that it is bilinear. Then, we know that there exists a linear map $V^*\otimes V\to \R$ which we call trace and is defined as

$${\rm tr}(f\otimes v) = \langle f, v\rangle = f(v).$$

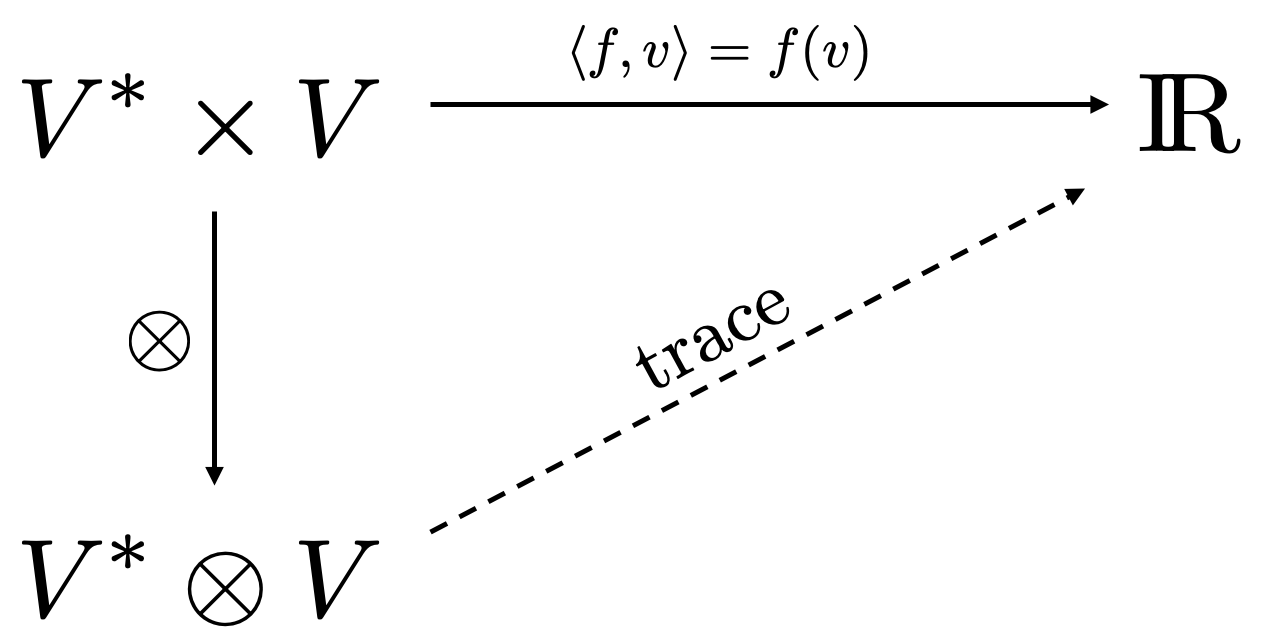
Figure 5. Trace definition using universal property.

References

1. Proof: Uniqueness of the Tensor Product, YouTube video by Mu Prime Math
2. Lecture notes on tensor products , accessed on 8 November 2023
3. Joel Kamnitzer, lecture notes on tensor products, accessed on 8 November 2023